Spatial Transform

坐标空间的变换

在渲染流水线中，我们往往需要把一个点或者方向矢量从一个坐标空间转换到另一个坐标空间，这个过程的是怎么实现的？
我们要想定义一个坐标空间，必须指明其原点位置和三个坐标轴的方向。而这些数值实际上是相对于另一个坐标空间的。也就是说坐标空间会形成一个层次结构——每个坐标空间都是另一个坐标空间的子空间，反过来说，每个空间都有一个父坐标空间。对坐标空间的变换实际上就是在父空间和子空间之间对点和矢量进行变换。
假设现在有父坐标空间P以及一个子坐标空间C，我们现在已知父坐标空间中子坐标空间的原点位置以及三个单位坐标轴。我们会有两种需求，一种需求是把子坐标空间下表示的点或矢量A_c转换到父坐标空间下的表示A_p，另一种需求是反过来，即把父坐标空间下表示的点或矢量B_p转换到子坐标空间下的表示B_c。我们可以用下面的公式来表示这两种需求：

$$
A_p = M_{c \rightarrow p}A_c
$$
$$
B_c = M_{p \rightarrow c}B_p
$$

其中，M_c->p表示的是从子坐标空间变换到父坐标空间的变换矩阵，M_p->c表示的是从父坐标空间变换到子坐标空间的变换矩阵，他俩互为逆矩阵。

下面我们就来讲解如何求出从子坐标空间到父坐标空间的变换矩阵M_c->p。

现在，我们已知子坐标空间C的3个坐标轴在父坐标空间P下的表示为：x_c、y_c、z_c，以及其原点位置O_c。当给定一个子坐标空间中的一个点A_c = (a,b,c)，我们可以用下面四个步骤来确定其在父坐标空间下的位置A_p：

1. 从坐标空间的原点开始
我们已经知道了子坐标空间的原点位置$O_c$。

2. 向 x 轴方向移动 a 个单位
我们已经知道了x轴的矢量表示，因此可以得到
$$
O_c + ax_c
$$

3. 向 y 轴方向移动 b 个单位
同样的道理，这一步就是：
$$
O_c + ax_c + by_c
$$

4. 向 z 轴方向移动 c 个单位
最后就可以得到
$$
O_c + ax_c + by_c + cz_c
$$

那么，

$$
\begin{aligned}
A_p
&= O_c + ax_c + by_c + cz_c\
&= (x_{O_c}, y_{O_c}, z_{O_c}) + a(x_{x_c}, y_{x_c}, z_{x_c}) + b(x_{y_c}, y_{y_c}, z_{y_c}) + c(x_{z_c}, y_{z_c}, z_{z_c})\
&= (x_{O_c}, y_{O_c}, z_{O_c}) +
\begin{bmatrix}
x_{x_c}&x_{y_c}&x_{z_c}\
y_{x_c}&y_{y_c}&y_{z_c}\
z_{x_c}&z_{y_c}&z_{z_c}\
\end{bmatrix}
\begin{bmatrix}a\b\c\\end{bmatrix}\
&= (x_{O_c}, y_{O_c}, z_{O_c}) +
\begin{bmatrix}
|&|&|\
x_c&y_c&z_c\
|&|&|\
\end{bmatrix}
\begin{bmatrix}a\b\c\\end{bmatrix}\
&= O_c + \begin{bmatrix}x_c&y_c&z_c\\end{bmatrix}\begin{bmatrix}a\b\c\\end{bmatrix}
\end{aligned}
$$

由于3 $\times$ 3的矩阵无法表示平移变换，我们把上面的式子扩展到齐次坐标空间中，得
$$
\begin{aligned}
A_p
&= (x_{O_c}, y_{O_c}, z_{O_c}, 1) +
\begin{bmatrix}
|&|&|&0\
x_c&y_c&z_c&0\
|&|&|&0\
0&0&0&1\
\end{bmatrix}
\begin{bmatrix}a\b\c\1\\end{bmatrix}\
&=\begin{bmatrix}
1&0&0&x_{O_c}\
0&1&0&y_{O_c}\
0&0&1&z_{O_c}\
0&0&0&1\
\end{bmatrix}
\begin{bmatrix}
|&|&|&0\
x_c&y_c&z_c&0\
|&|&|&0\
0&0&0&1\
\end{bmatrix}
\begin{bmatrix}a\b\c\1\\end{bmatrix}\
&= \begin{bmatrix}
|&|&|&x_{O_c}\
x_c&y_c&z_c&y_{O_c}\
|&|&|&z_{O_c}\
0&0&0&1\
\end{bmatrix}
\begin{bmatrix}a\b\c\1\\end{bmatrix}\
\end{aligned}
$$

所以，显而易见
$$
M_{c \rightarrow p} =
\begin{bmatrix}
|&|&|&x_{O_c}\
x_c&y_c&z_c&y_{O_c}\
|&|&|&z_{O_c}\
0&0&0&1\
\end{bmatrix}
$$

可以看出来，变换矩阵M_c->p实际上可以通过坐标空间C在坐标空间P中的原点和坐标轴的矢量表示来构建出来：把3个坐标轴依次放入矩阵的前三列，把原点矢量放到最后一列，再用0和1填充最后一行即可。

我们可以利用反向思维，从这个变换矩阵反推来获取子坐标空间的原点和坐标轴方向。例如，当我们已知从模型空间到世界空间的一个4 $\times$ 4的变换矩阵，可以提取它的第一列再进行归一化后（为了消除缩放的影响）来得到模型空间的x轴在世界空间下的单位矢量表示。同样的方法可以提取y轴和z轴。我们可以从另一个角度来理解这个提取过程。因为矩阵M_c->p可以把一个方向矢量从坐标空间C变换到坐标空间P中，那么，只需要用它来变换坐标空间C中的x轴(1,0,0,0),即使用矩阵乘法
$$
M_{c \rightarrow p}
\begin{bmatrix}
1&0&0&0
\end{bmatrix}^T
$$
得到的结果正是M_c->p的第一列。

对矢量的坐标空间变换可以使用3 $\times$ 3的矩阵来表示，因为我们不需要表示平移变换，在Shader中，我们常常会看到截取变换矩阵的前3行前3列来对法线方向、光照方向来进行空间变换，这正是原因所在。

由于M_c->p和M_p->c互为逆矩阵，我们可以通过求M_c->p的逆矩阵的方式来求出M_p->c，但当M_c->p是一个正交矩阵时，M_c->p的逆矩阵就等于它的转置矩阵，也就是说，
$$
\begin{aligned}
M_{p \rightarrow c} &=
\begin{bmatrix}
|&|&|\
x_p&y_p&z_p\
|&|&|\
\end{bmatrix}
= M_{c \rightarrow p}^{-1} = M_{c \rightarrow p}^T\
&=
\begin{bmatrix}
-&x_c&-\
-&y_c&-\
-&z_c&-\
\end{bmatrix}
\end{aligned}
$$
现在，我们不仅可以根据变换矩阵M_c->p反推出子坐标空间的坐标轴方向在父坐标空间中的表示x_c、y_c和z_c，还可以反推出父坐标空间的坐标轴方向在子坐标空间中的表示x_p、y_p和z_p

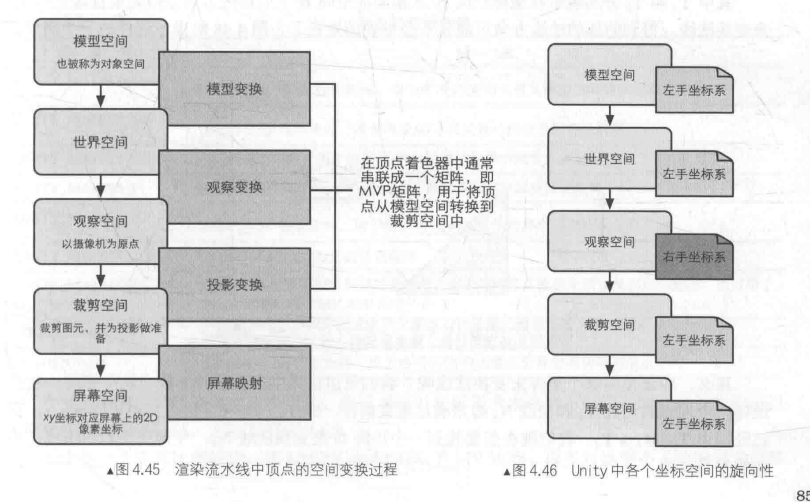
顶点的坐标空间变换过程

法线变换

法线(normal)，也被称为法矢量(normal vector)。在上面我们已经看到如何使用变换矩阵来变换一个顶点或一个方向矢量，但法线是需要我们特殊处理的一种方向矢量。在游戏中，模型的一个顶点往往会携带额外的信息，而顶点法线就是其中一种信息。当我们变换一个模型的时候，不仅需要变换它的顶点，还需要变换顶点法线，以便在后续处理(如片元着色器)中计算光照等。

一般来说，点和绝大部分方向矢量都可以使用同一个4 $\times$ 4或3 $\times$ 3的变换矩阵M_A->B把其从坐标空间A变换到坐标空间B中。但在变换法线的时候，如果使用同一个变换矩阵，可能就无法确保维持法线的垂直性。下面就来了解一下为什么会出现这样的问题。

我们先来了解一下另一种方向矢量——切线(tangent)，也被称为切矢量(tangent vector)。与法线类似，切线往往也是模型顶点携带的一种信息。它通常与纹理空间对齐，且与法线方向垂直。

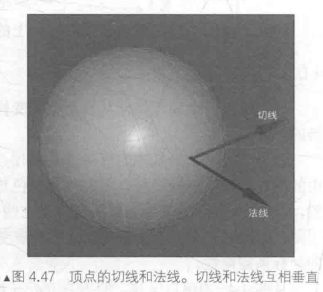
由于切线是由两个顶点之间的差值计算得到的，因此我们可以直接使用用于变换顶点的变换矩阵来变换切线。假设，我们使用3 $\times$ 3的变换矩阵M_A->B来变换顶点(注意，这里涉及的变换矩阵都是3 $\times$ 3的矩阵，不考虑平移变换。这是因为切线和法线都是方向矢量，不会受平移的影响)，可以由下面的式子直接得到变换后的切线：
$$
T_B = M_{A \rightarrow B}T_A
$$
其中T_A和T_B分别表示在坐标空间A和坐标空间B下的切线方向。但如果直接使用M_A->B来变换法线，得到的新的法线方向可能就不会与表面垂直了。

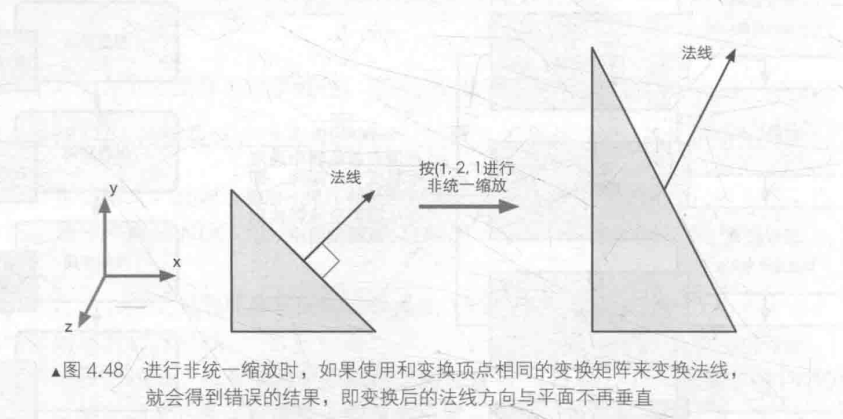
我们可以由数学约束条件来推出正确变换法线的矩阵。我们知道同一个顶点的切线T_A和法线N_A必须满足垂直条件，即 $T_A \cdot N_A = 0$。给定变换矩阵M_A->B，我们已经知道 $T_B = M_{A \rightarrow B}T_A$。我们现在想要找到一个矩阵G来变换法线N_A，使得变换后的法线仍然与切线垂直。即
$$
T_B \cdot N_B = (M_{A \rightarrow B}T_A) \cdot (GN_A) = 0
$$

对上式进行一些推导后可得
$$
(M_{A \rightarrow B}T_A) \cdot (GN_A) = (M_{A \rightarrow B}T_A)^T(GN_A) = T_A^TM_{A \rightarrow B}^TGN_A = T_A^T(M_{A \rightarrow B}^TG)N_A = 0
$$

由于 $T_A \cdot N_A = 0$，因此如果$M_{A \rightarrow B}^TG = I$，那么上式即可成立。也就是说，如果 $G = (M_{A \rightarrow B}^T)^{-1} = (M_{A \rightarrow B}^{-1})^T$，即使用原变换矩阵的逆转置矩阵来变换法线就可以得到正确的结果。

值得注意的是，如果变换矩阵M_A->B是正交矩阵，那么 $M_{A \rightarrow B}^{-1} = M_{A \rightarrow B}^T$，因此$(M_{A \rightarrow B}^T)^{-1} = M_{A \rightarrow B}$，也就是说我们可以使用用于变换顶点的变换矩阵来直接变换法线。如果变换只包括旋转变换，那么这个变换矩阵就是正交矩阵。而如果变换只包含旋转和统一缩放，而不包含非统一缩放，我们利用统一缩放系数k来得到变换矩阵M_A->B的逆转置矩阵
$(M_{A \rightarrow B}^T)^{-1} = \frac {1} {k} M_{A \rightarrow B}$。这样就可以避免计算逆矩阵的过程。如果变换中包含了非统一变换，那么我们就必须要求解逆矩阵来得到变换法线的矩阵。

参考

《Unity Shader入门精要》