Delaunay-Triangulation

Delaunay 三角形化

Delaunay三角形化，也叫Delaunay三角剖分，是一种三角剖分算法，它的作用是把一个平面上的点集，按照一定的规则，分成若干个三角形。这些三角形有以下特点：

• 这些三角形互不重叠
• 这些三角形可以覆盖整个平面
• 每个点均不位于不包含该点的三角形的外接圆内（即：在某个三角形的外接圆内，只包含在外接圆上的三个点，不包含其他点）

Delaunay 三角形化的优点：

• 最小角的最大化（所形成的最小角是所有连接方式形成的最小角中的最大者）
• 生成的三角形边长的均匀性最好，最接近正三角形

Delaunay 三角形化方法

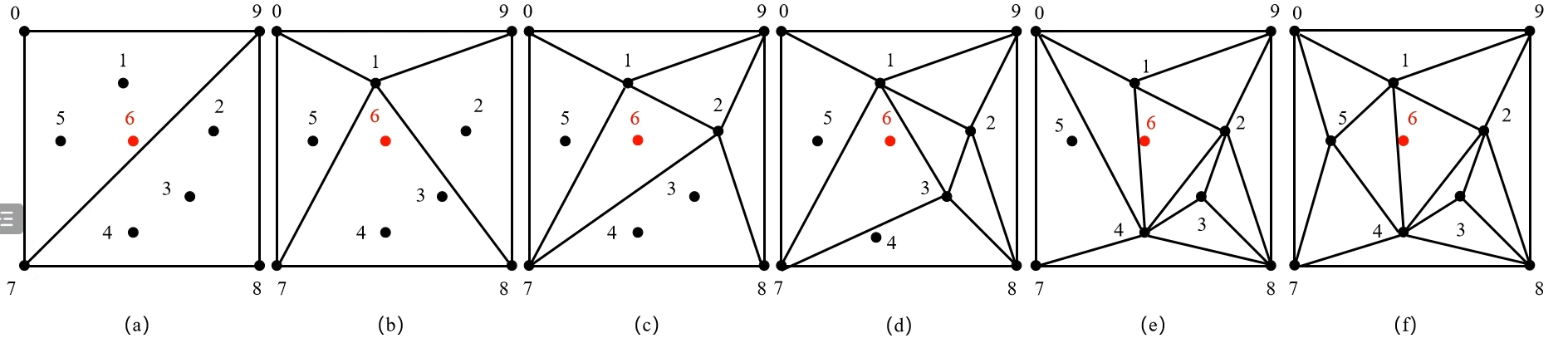
如上图所示的求解区域为例，1~5是边界点，6为内部点，其初始化 Delaunay 三角形的过程如下：

1. 包围该求解区域的各边界点做一个辅助正四边形及两个三角形 $\triangle{790}$，$\triangle{789}$，显然这两个三角形为 Delaunay 三角形；
2. 首先考虑节点1，它位于$\triangle{790}$和$\triangle{789}$的外接圆内；
3. 消去公共线79，连接点1与四个顶点（0，7，8，9）；
4. 考虑点2，它位于$\triangle{178}$和$\triangle{189}$的外接圆内；
5. 消去公共线18，连接点2与四个顶点（1，7，8，9）；
6. 采用同样的方法依次考虑点3、4、5，最后形成图（f）所示情况，注意不一定位于两个外接圆内，可能更多，即公共线也更多

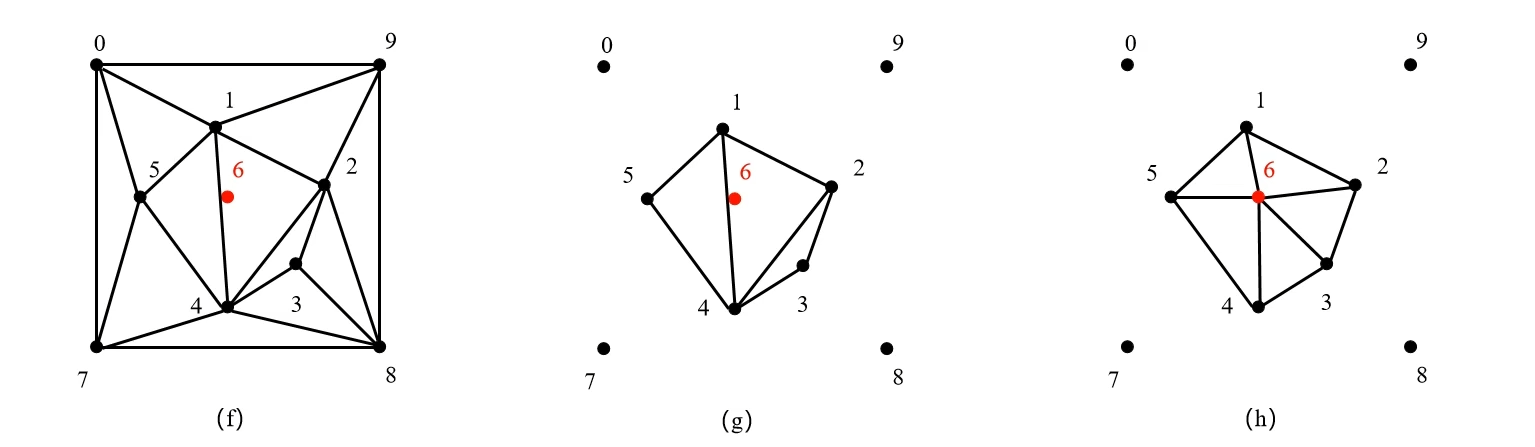
7. 删除所有重心不在求解区域的三角形得到图（g）所示的初始化 Delaunay 三角形；
8. 由于点6为内部点，它位于$\triangle{145}$、$\triangle{142}$ 和 $\triangle{234}$ 外接圆内，因此需要消去公共线14、24，连接点6与五个顶点（1，2，3，4，5）；

如何向求解区域内设点

为了能方便控制区域内点附近网格的疏密，引入两个几何参数

1. 长度标尺，长度标尺的大小代表边界上网格疏密的程度，网格点越稠密的地方，长度标尺越小，网格点越稀疏的地方，长度标尺越大；
2. 三角形外接圆无量纲半径，判断三角形偏离正三角形的严重程度，$R(k)$越大偏离越严重，首先应该往$R(k)$较大的三角形中添加点以改善网格质量；

长度标尺

长度标尺是赋予网格点的一个几何参数

边界网格点的长度标尺定义为：该点到边界上相邻两个边界网格点的距离的平均值的 $\sqrt{3}/2$ 倍；如点1的长度标尺为：(点1到点2的距离 + 点1到点5的距离)/2 * $\sqrt{3}/2$

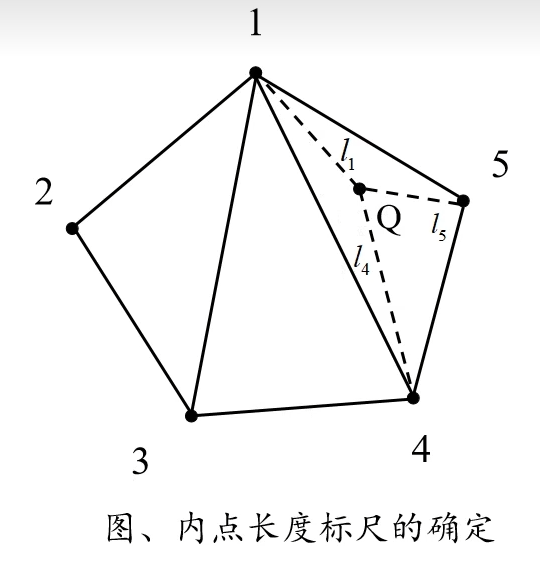
内部网格点的长度标尺采用下列倒数原则，由边界网格点的长度标尺插值而得；设Q点是要插入到$\triangle{145}$中的一点，则：

$$L(Q) = \frac{L(1)/l_1 + L(4)/l_4 + L(5)/l_5}{1/l_1 + 1/l_4 + 1/l_5}$$

式中，$L(1)$，$L(4)$，$L(5)$ 分别为点1，点4，点5的长度标尺，$l_1$, $l_4$, $l_5$ 分别为点Q到点1，点4，点5的距离；

三角形外接圆无量纲半径

设任意一个 Delaunay 三角形为 $\triangle{k}$，其外接圆的半径为 $r(k)$，其外接圆的圆心长度标尺为 $L(k)$，则其外接圆无量纲半径 $R(k)$ 为：

$$R(k) = \frac{r(k)}{L(k)}$$

正三角形的外接圆无量纲半径最小，值为2/3

步骤

1. 计算所有已生成的 Delaunay 三角形的外接圆圆心的长度标尺 $L(k)$ 以及外接圆半径 $r(k)$；
2. 计算所有三角形的外接圆无量纲半径 $R(k)$；
3. 对所有现存三角形按 $R(k)$ 从大到小排序；
4. 在 $R(k)$ 最大的三角形的外接圆圆心处添加新的点Q；
5. 利用 Delaunay 三角形化方法，生成一组新的 Delaunay 三角形；
6. 返回第一步，重复加点动作，直到满足要求；