深度和法线纹理

本文最后更新于：2025年4月17日 下午

获取深度和法线纹理

背后的原理

深度纹理实际上就是一张渲染纹理，只不过它里面存储的像素值不是颜色值，而是一个高精度的深度值。由于被存储在一张纹理中，深度纹理里的深度值范围是[0, 1]，而且通常是非线性分布的。这些深度值来自于顶点变换后得到的归一化的设备坐标（Normalized Device Coordinates，NDC）。想要在屏幕上绘制一个模型，需要把模型顶点在顶点着色器中乘以 MVP 变换矩阵，将顶点从模型空间变换到齐次裁剪坐标系下。在变换的最后一步，我们使用一个投影矩阵来变换顶点，如果我们使用的是透视投影类型的摄像机，那这个投影矩阵就是非线性的。

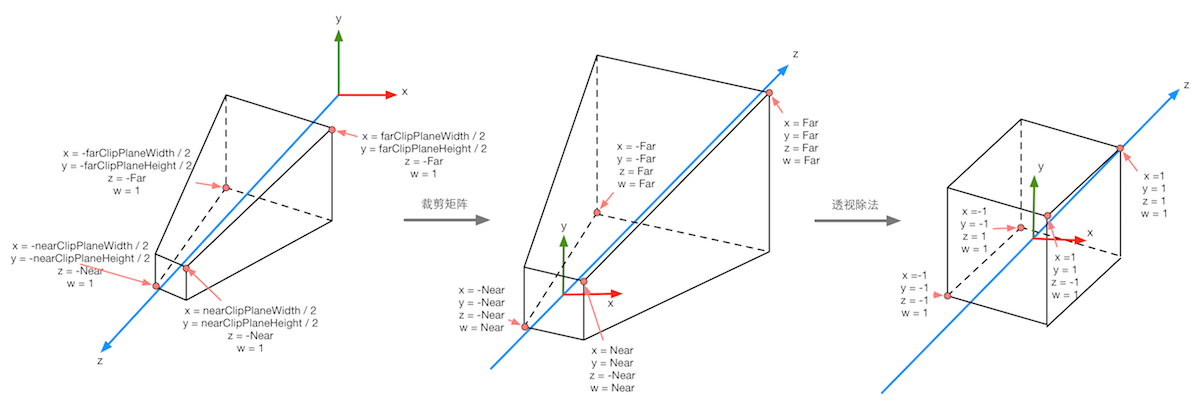
下图显示了 Unity 中透视投影对顶点的变换过程。最左侧的图显示了投影变换前，即观察空间下视锥体的结构及相应的顶点位置，中间的图显示了应用透视裁剪矩阵后的变换结果，即顶点着色器阶段输出的顶点变换结果，最右侧的图则是底层硬件进行了透视除法后得到的归一化的设备坐标。需要注意的是，这里的投影过程是建立在 Unity 对坐标系的假定上的，也就是说，我们针对的是观察空间为右手坐标系，使用列矩阵在矩阵右侧进行相乘，且变换到 NDC 后 z 分量范围将在[-1, 1]之间的情况。而在类似 DirectX 这样的图形接口中，变换后 z 分量范围将在[0, 1]之间。如果需要在其他图形接口下实现本章的类似效果，需要对一些计算参数做出相应变化。

透视投影

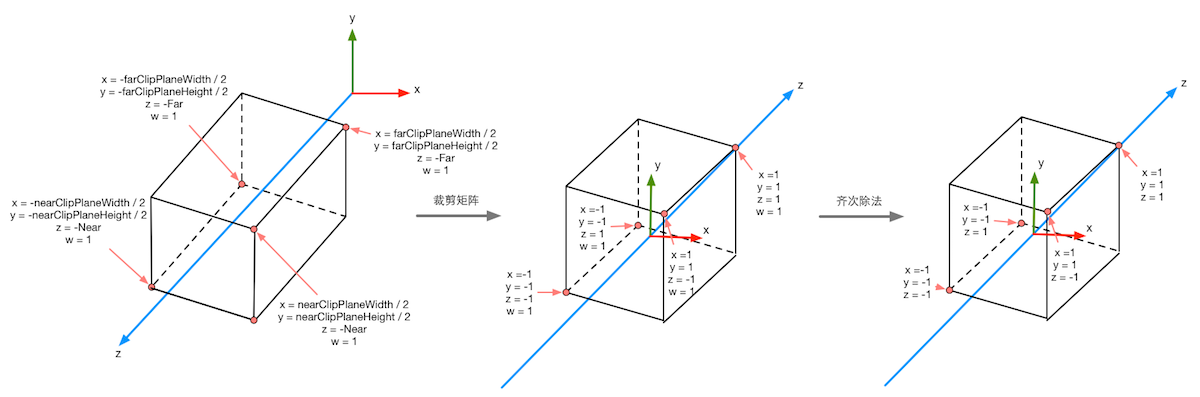
下图显示了在使用正交摄像机时投影变换的过程。同样，变换后会得到一个范围为[-1, 1]的立方体。正交投影使用的变换矩阵是线性的。

正交投影

在得到 NDC 后，深度纹理中的像素值就可以很方便地计算得到了，这些深度值就对应了 NDC 中顶点坐标的 z 分量的值。由于 NDC 中 z 分量的范围在[-1, 1]，为了让这些值能够存储在一张图像中，我们需要使用下面的公式对其进行映射：
$$
d = 0.5 \cdot z_{ndc} + 0.5
$$
其中，$d$ 对应了深度纹理中的像素值，$z_{ndc}$ 对应了 NDC 坐标中的 z 分量的值。

那么 Unity 如何得到这样一张深度纹理呢？在 Unity 中，深度纹理可以直接来自于真正的深度缓存，也可以由一个单独的 Pass 渲染而得，这取决于使用的渲染路径和硬件。通常来讲，当使用延迟渲染路径（包括遗留的渲染路径）时，深度纹理理所当然的可以访问到，因为延迟渲染会把这些信息渲染到 G-buffer 中。而当无法直接获取深度缓存时，深度和法线纹理是通过一个单独的 Pass 渲染而得的。具体实现是，Unity 会使用着色器替换（Shader Replacement）技术选择那些渲染类型（即 SubShader 的 RenderType 标签）为 Opaque 的物体，判断它们使用的渲染队列是否小于等于 2500（内置的 Background、Geometry 和 AlphaTest 渲染队列均在此范围内），如果满足条件，就把它渲染到深度和法线纹理中。因此，想要让物体能够出现在深度和法线纹理中，就必须在 Shader 中设置正确的 RenderType 标签。

在 Unity 中，我们可以选择让一个摄像机生成一张深度纹理或是一张深度+法线纹理。当只需要一张单独的深度纹理时，Unity 会直接获取深度缓存或是按之前讲到的着色器替换技术，选取需要的不透明物体，并使用它投射阴影时使用的 Pass（即 LightMode 被设置为 ShadowCaster 的 Pass）来得到深度纹理。如果 Shader 中不包含这样一个 Pass，那么这个物体就不会出现在深度纹理中（当然，它也不能向其他物体投射阴影）。深度纹理的精度通常是 24 位或 16 位，这取决于使用的深度缓存的精度。如果选择生成一张深度+法线纹理，Unity 会创建一张和屏幕分辨率相同、精度为 32 位（每个通道为 8 位）的纹理，其中观察空间下的法线信息会被编码进纹理的 R 和 G 通道，而深度信息会被编码进 B 和 A 通道。法线信息的获取在延迟渲染中是可以非常容易就得到的，Unity 只需要合并深度和法线缓存即可。而在前向渲染中，默认情况下是不会创建法线缓存的，因此 Unity 底层使用了一个单独的 Pass 把整个场景再次渲染一遍来完成。

如何获取

在 Unity 中，获取深度纹理是非常简单的，我们在脚本中设置摄像机的 depthTextureMode 后，就可以在 Shader 中直接访问特定的纹理属性。例如我们可以通过下面的代码来获取深度纹理：

1
camera.depthTextureMode = DepthTextureMode.Depth;

一旦设置好了上面的摄像机模式后，我们就可以在 Shader 中通过声明 _CameraDepthTexture 变量来访问它。

同理，如果想要获取深度+法线纹理，我们只需要在代码中这样设置：

1
camera.depthTextureMode = DepthTextureMode.DepthNormals;

然后在 Shader 中通过声明 _CameraDepthNormalsTexture 变量来访问它。

我们还可以组合这些模式，让一个摄像机同时产生一张深度和深度+法线纹理：

1
2
camera.depthTextureMode |= DepthTextureMode.Depth;
camera.depthTextureMode |= DepthTextureMode.DepthNormals;

我们还可以在摄像机的 Camera 组件上看到当前摄像机是否需要渲染深度或深度+法线纹理。当在 Shader 中访问到深度纹理 _CameraDepthTexture 后，我们就可以使用当前像素的纹理坐标对它进行采样。绝大多数情况下，我们直接使用 tex2D 函数采样即可，但在某些平台（例如 PS3 和 PSP2 ）上，我们需要一些特殊处理。Unity 为我们提供了一个统一的宏 SAMPLE_DEPTH_TEXTURE，用来处理这些由于平台差异造成的问题。而我们只需要在 Shader 中使用 SAMPLE_DEPTH_TEXTURE 宏对深度纹理进行采样，例如：

1
float d = SAMPLE_DEPTH_TEXTURE(_CameraDepthTexture, i.uv);

其中，i.uv 是一个 float2 类型的变量，对应了当前像素的纹理坐标。类似的宏还有 SAMPLE_DEPTH_TEXTURE_PROJ 和 SAMPLE_DEPTH_TEXTURE_LOD。SAMPLE_DEPTH_TEXTURE_PROJ 宏同样接受两个参数——深度纹理和一个 float3 或 float4 类型的纹理坐标，它的内部使用了 tex2Dproj 这样的函数进行投影纹理采样，纹理坐标的前两个分量首先会除以最后一个分量，再进行纹理采样。如果提供了第四个分量，还会进行一次比较，通常用于阴影的实现中。SAMPLE_DEPTH_TEXTURE_PROJ 的第二个参数通常是由顶点着色器输出插值而得的屏幕坐标，例如：

1
float d = SAMPLE_DEPTH_TEXTURE_PROJ(_CameraDepthTexture, UNITY_PROJ_COORD(i.scrPos));

其中，i.scrPos 是在顶点着色器中通过调用 ComputeScreenPos(o.pos) 得到的屏幕坐标。上述这些宏的定义我们可以在 Unity 内置的 HLSLSupport.cginc 文件中找到。

当通过纹理采样得到深度值后，这些深度值往往是非线性的，这种非线性来自于透视投影使用的裁剪矩阵。然而，在我们的计算过程中通常需要线性的深度值，因此我们需要把投影后的深度值变换到线性空间下，例如视角空间下的深度值。那么，我们应该如何进行这个转换呢？实际上，我们只需要倒推顶点变换的过程即可。下面我们以透视投影为例，推导如何由深度纹理中的深度信息计算得到视角空间下的深度值。

当我们使用透视投影的裁剪矩阵 $P_{clip}$ 对视角空间下的一个顶点进行变换后，裁剪空间下的顶点的 z 和 w 分量为：

$$
z_{clip} = -z_{view}\frac{Far + Near}{Far - Near} - \frac{2 \cdot Near \cdot Far}{Far - Near}
$$
$$
w_{clip} = -z_{view}
$$

其中，$Far$ 和 $Near$ 分别是远近裁剪平面的距离。然后，我们通过齐次除法就可以得到 NDC 下的 z 分量：

$$
z_{ndc} = \frac{z_{clip}}{w_{clip}} = \frac{Far + Near}{Far - Near} + \frac{2 \cdot Near \cdot Far}{(Far - Near) \cdot z_{view}}
$$

深度纹理中的深度值是通过下面的公式由 NDC 计算而得的：
$$
d = 0.5 \cdot z_{ndc} + 0.5
$$
由上面的这些式子，我们可以推导出用 $d$ 表示而得的 $z_{view}$ 的表达式：
$$
z_{view} = \frac{1}{\frac{Far - Near}{Near \cdot Far}d - \frac{1}{Near}}
$$
由于在 Unity 使用的视角空间中，摄像机正向对应的 z 值均为负值，因此为了得到深度值的正数表示，我们需要对上面的结果取反，最后得到的结果如下：
$$
z_{view}^{'} = \frac{1}{\frac{Near - Far}{Near \cdot Far}d + \frac{1}{Near}}
$$
它的取值范围就是视锥体深度范围，即[Near, Far]。如果我们想得到范围在[0, 1]之间的深度值，只需要把上面得到的结果除以 Far 即可。这样，0 就表示该点与摄像机位于同一位置，1 表示该点位于视锥体的远裁剪平面上。结果如下：
$$
z_{01} = \frac{1}{\frac{Near - Far}{Near}d + \frac{Far}{Near}}
$$

Unity 提供了两个辅助函数来为我们进行上述的计算过程——LinearEyeDepth 和 Linear01Depth。LinearEyeDepth 负责把深度纹理采样结果转换到视角空间下的深度值，也就是我们上面得到的 $z_{view}^{'}$。而 Linear01Depth 则会返回一个范围在[0, 1]的线性深度值，也就是我们上面得到的 $z_{01}$。这两个函数内部使用了内置的 _ZBufferParams 变量来得到远近裁剪平面的距离。

如果我们需要获取深度+法线纹理，可以直接使用 tex2D 函数对 _CameraDepthNormalsTexture 进行采样，得到里面存储的深度和法线信息。Unity 提供了辅助函数来为我们对这个采样结果进行解码，从而得到深度值和法线方向。这个函数是 DecodeDepthNormal，它在 UnityCG.cginc 里被定义：

1
2
3
4
inline void DecodeDepthNormal(float4 enc, out float depth, out float3 normal){
    depth = DecodeFloatRG(enc.zw);
    normal = DecodeViewNormalStereo(enc);
}

DecodeDepthNormal 的第一个参数是对深度+法线纹理的采样结果，这个采样结果是 Unity 对深度和法线信息编码后的结果，它的 xy 分量存储的是视角空间下的法线信息，而深度信息被编码进了 zw 分量。通过调用 DecodeDepthNormal 函数对采样结果解码后，我们就可以得到解码后的深度值和法线。这个深度值是范围在[0, 1]的线性深度值（这与单独的深度纹理中存储的深度值不同），而得到的法线则是视角空间下的法线方向。同样，我们也可以通过调用 DecodeFloatRG 和 DecodeViewNormalStereo 来解码深度+法线纹理中的深度和法线信息。

查看深度和法线纹理

下图显示了使用帧调试器查看到的深度纹理和深度+法线纹理。

帧调试器查看深度和法线纹理

使用帧调试器查看到的深度纹理是非线性空间的深度值，而深度+法线纹理都是由 Unity 编码后的结果。有时，显示出线性空间下的深度信息或解码后的法线方向会更加有用。此时，我们可以自行在片元着色器中输出转换或解码后的深度和法线值，如下图示。

线性空间下的深度纹理和解码后并被映射到[0, 1]范围内的视角空间下的法线纹理

我们可以使用类似下面的代码来输出线性深度值：

1
2
3
float depth = SAMPLE_DEPTH_TEXTURE(_CameraDepthTexture, i.uv);
float linearDepth = Linear01Depth(depth);
return fixed4(linearDepth, linearDepth, linearDepth, 1.0);

或是输出法线方向：

1
2
fixed3 normal = DecodeViewNormalStereo(tex2D(_CameraDepthNormalsTexture, i.uv).xy);
return fixed4(normal * 0.5 + 0.5, 1.0);

在查看深度纹理时，得到的画面有可能几乎是全黑或全白的。这时候可以把摄像机的远裁剪平面的距离（Unity 默认为 1000）调小，使视锥体的范围刚好覆盖场景的所在区域。这是因为，由于投影变换时需要覆盖从近裁剪平面到远裁剪平面的所有深度区域，当远裁剪平面的距离过大时，就会导致离摄像机较近的距离被映射到非常小的深度值，如果场景是一个封闭的区域（如上图所示），那么这就会导致画面看起来几乎是全黑的。相反，如果场景是一个开放区域，且物体离摄像机的距离较远，就会导致画面几乎是全白的。

再谈运动模糊

我们以前学习了如何通过混合多张屏幕图像来模拟运动模糊的效果。但是，另一种应用更加广泛的技术则是使用速度映射图。速度映射图中存储了每个像素的速度，然后使用这个速度来决定模糊的方向和大小。速度缓冲的生成有多种方法，一种方法是把场景中所有物体的速度渲染到一张纹理中。但这种方法的缺点在于需要修改场景中所有物体的 Shader 代码，使其添加计算速度的代码并输出到一个渲染纹理中。

《GPU Gems3》在第27章中介绍了一种生成速度映射图的方法。这种方法利用深度纹理在片元着色器中为每个像素计算其在世界空间下的位置，这是通过使用当前的视角 * 投影矩阵的逆矩阵对 NDC 下的顶点坐标进行变换得到的。当得到世界空间中的顶点坐标后，我们使用前一帧的视角 * 投影矩阵对其进行变换，得到该位置在前一帧中的 NDC 坐标。然后，我们计算前一帧和当前帧的位置差，生成该像素的速度。这种方法的优点是可以在一个屏幕后处理步骤中完成整个效果的模拟，但缺点是需要在片元着色器中进行两次矩阵乘法的操作，对性能有所影响。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
using UnityEngine;
using System.Collections;

public class MotionBlurWithDepthTexture : PostEffectsBase {

	public Shader motionBlurShader;
	private Material motionBlurMaterial = null;

	public Material material {  
		get {
			motionBlurMaterial = CheckShaderAndCreateMaterial(motionBlurShader, motionBlurMaterial);
			return motionBlurMaterial;
		}  
	}

	private Camera myCamera;
	public Camera camera {
		get {
			if (myCamera == null) {
				myCamera = GetComponent<Camera>();
			}
			return myCamera;
		}
	}

	[Range(0.0f, 1.0f)]
	public float blurSize = 0.5f;

	private Matrix4x4 previousViewProjectionMatrix;
	
	void OnEnable() {
		camera.depthTextureMode |= DepthTextureMode.Depth;

		previousViewProjectionMatrix = camera.projectionMatrix * camera.worldToCameraMatrix;
	}
	
	void OnRenderImage (RenderTexture src, RenderTexture dest) {
		if (material != null) {
			material.SetFloat("_BlurSize", blurSize);

			material.SetMatrix("_PreviousViewProjectionMatrix", previousViewProjectionMatrix);
			Matrix4x4 currentViewProjectionMatrix = camera.projectionMatrix * camera.worldToCameraMatrix;
			Matrix4x4 currentViewProjectionInverseMatrix = currentViewProjectionMatrix.inverse;
			material.SetMatrix("_CurrentViewProjectionInverseMatrix", currentViewProjectionInverseMatrix);
			previousViewProjectionMatrix = currentViewProjectionMatrix;

			Graphics.Blit (src, dest, material);
		} else {
			Graphics.Blit(src, dest);
		}
	}
}

上面的 OnRenderImage 函数很简单，我们首先需要计算和传递运动模糊使用的各个属性。本例需要使用两个变换矩阵——前一帧的视角 * 投影矩阵以及当前帧的视角 * 投影矩阵的逆矩阵。因此，我们通过调用 camera.worldToCameraMatrix 和 camera.projectionMatrix 来分别得到当前摄像机的视角矩阵和投影矩阵。对它们相乘后取逆，得到当前帧的视角 * 投影矩阵的逆矩阵，并传递给材质。然后，我们把取逆前的结果存储在 previousViewProjectionMatrix 变量中，以便在下一帧时传递给材质的 _PreviousViewProjectionMatrix 属性。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
Shader "Custom/Chapter13/Chapter13-MotionBlurWithDepthTexture" {

    Properties {
        _MainTex ("Base (RGB)", 2D) = "white" {}
        _BlurSize ("Blur Size", Float) = 1.0
    }

    SubShader {
        CGINCLUDE
        #include "UnityCG.cginc"

        sampler2D _MainTex;
        half4 _MainTex_TexelSize;
        sampler2D _CameraDepthTexture;
        float4x4 _CurrentViewProjectionInverseMatrix;
        float4x4 _PreviousViewProjectionMatrix;
        half _BlurSize;


        struct v2f {
            float4 pos : SV_POSITION;
            half2 uv : TEXCOORD0;
            half2 uv_depth : TEXCOORD1;
        };

        v2f vert(appdata_img v) {
            v2f o;
            o.pos = UnityObjectToClipPos(v.vertex);

            o.uv = v.texcoord;
            o.uv_depth = v.texcoord;

            #if UNITY_UV_STARTS_AT_TOP
            if (_MainTex_TexelSize.y < 0)
                o.uv_depth.y = 1 - o.uv_depth.y;
            #endif

            return o;
        }

        fixed4 frag(v2f i) : SV_Target {
            //Get the depth buffer value at this pixel.
            float d = SAMPLE_DEPTH_TEXTURE(_CameraDepthTexture, i.uv_depth);
            //H is the viewport position at this pixel in the range -1 to 1.
            float4 H = float4(i.uv.x * 2 - 1, i.uv.y * 2 - 1, d * 2 - 1, 1);
            //Transform by the view-projection inverse
            float4 D = mul(_CurrentViewProjectionInverseMatrix, H);
            //Divide by w to get the world position.
            float4 worldPos = D / D.w;

            //current viewport position
            float4 currentPos = H;
            //Use the world position, and transform by the previous view-projection matrix.
            float4 previousPos = mul(_PreviousViewProjectionMatrix, worldPos);
            //Convert to nonhomogeneous points [-1, 1] by dividing by w.
            previousPos /= previousPos.w;

            //Use this frame's position and last frame's to compute the pixel velocity.
            float2 velocity = (currentPos.xy - previousPos.xy) / 2.0f;

            float2 uv = i.uv;
            float4 c = tex2D(_MainTex, uv);
            uv += velocity * _BlurSize;
            for (int it = 1; it < 3; it++, uv += velocity * _BlurSize) {
                float4 currentColor = tex2D(_MainTex, uv);
                c += currentColor;
            }
            c /= 3;

            return fixed4(c.rgb, 1.0);
        }
        ENDCG

        Pass {
            ZTest Always Cull Off ZWrite Off
            CGPROGRAM
            #pragma vertex vert
            #pragma fragment frag
            ENDCG
        }
    }

    FallBack Off
}

_MainTex 对应了输入的渲染纹理，_BlurSize 是模糊图像时使用的参数。虽然在脚本里设置了材质的 _PreviousViewprojectionMatrix 和 _CurrentViewProjectionInverseMatrix 属性，但并没有在 Properties 块中声明它们。这是因为 Unity 没有提供矩阵类型的属性，但我们仍然可以在 CG 代码块中定义这些矩阵，并从脚本中设置它们。

除了定义在 Properties 声明的 _MainTex 和 _BlurSize 属性，我们还声明了其他三个变量。_CameraDepthTexture 是 Unity 传递给我们的深度纹理，而 _CurrentViewProjectionInverseMatrix 和 _PreviousViewProjectionMatrix 是由脚本传递而来的矩阵。除此之外，我们还声明了 _MainTex_TexelSize 变量，它对应了主纹理的纹素大小，我们需要使用该变量来对深度纹理的采样坐标进行平台差异化处理。

由于在本例中，我们需要同时处理多张渲染纹理，因此在 DirectX 这样的平台上，我们需要处理平台差异导致的图像翻转问题。在上面的代码中，我们对深度纹理的采样坐标进行了平台差异化处理，以便在类似 DirectX 的平台上，在开启了抗锯齿的情况下仍然可以得到正确的结果。

我们首先需要利用深度纹理和当前帧的视角 * 投影矩阵的逆矩阵来求得该像素在世界空间下的坐标。过程开始于对深度纹理的采样，我们使用内置的 SAMPLE_DEPTH_TEXTURE 宏和纹理坐标对深度纹理进行采样，得到了深度值 $d$。$d$ 是由 NDC 下的坐标映射而来的。我们想要构建像素的 NDC 坐标 $H$，就需要把这个深度值重新映射回 NDC。这个映射很简单，只需要使用原映射的反函数即可，即 $d$ * 2 - 1。同样，NDC 的 xy 分量可以由像素的纹理坐标映射而来（NDC 下的 xyz 分量范围均为[-1, 1]）。当得到 NDC 下的坐标 $H$ 后，我们就可以使用当前帧的视角 * 投影矩阵的逆矩阵对其进行变换，并把结果值除以它的 w 分量来得到世界空间下的坐标表示 worldPos。

一旦得到了世界空间下的坐标，我们就可以使用前一帧的视角 * 投影矩阵对它进行变换，得到前一帧在 NDC 下的坐标 previousPos。然后，我们计算前一帧和当前帧在屏幕空间下的位置差，得到该像素的速度 velocity。当得到该像素的速度后，我们就可以使用该速度值对它的邻域像素进行采样，相加后取平均值得到一个模糊的效果。采样时我们还使用了 _BlurSize 来控制采样距离。

本次实现的运动模糊适用于场景静止、摄像机快速运动的情况，这是因为我们在计算时只考虑了摄像机的运动。因此，如果把这些代码应用到一个物体快速运动而摄像机静止的场景，会发现不会产生任何运动模糊效果。如果我们想要对快速移动的物体产生运动模糊的效果，就需要生成更加精确的速度映射图。我们可以在 Unity 自带的 ImageEffect 包中找到更多的运动模糊的实现方法。

本次选择在片元着色器中使用逆矩阵来重建每个像素在世界空间下的位置。但是，这种做法往往会影响性能，下面我们会介绍一种更快速的由深度纹理重建世界坐标的方法。

全局雾效

**雾效（Fog）**是游戏里经常使用的一种效果。Unity 内置的雾效可以产生基于距离的线性或指数雾效。然而，要想在自己编写的顶点/片元着色器中实现这些雾效，我们需要在 Shader 中添加 #pragma multi_compile_fog 指令，同时还需要使用相关的内置宏，例如 UNITY_FOG_COORDS、UNITY_TRANSFER_FOG 和 UNTIY_APPLY_FOG 等。这种方法的缺点在于，我们不仅需要为场景中所有物体添加相关的渲染代码，而且能够实现的效果也非常有限。当我们需要对雾效进行一些个性化操作时，例如使用基于高度的雾效等，仅仅使用 Unity 内置的雾效就变得不再可行。

我们将学习一种基于屏幕后处理的全局雾效的实现。使用这种方法，我们不需要更改场景内渲染的物体所使用的 Shader 代码，而仅仅依靠一次屏幕后处理的步骤即可。这种方法的自由性很高，我们可以方便地模拟各种雾效，例如均匀的雾效、基于距离的线性/指数雾效等。在学习完本节后，我们可以得到类似下图中的效果。

全局雾效

基于屏幕后处理的全局雾效的关键是，根据深度纹理来重建每个像素在世界空间下的位置。尽管我们在模拟运动模糊时已经实现了这个要求，即构建出当前像素的 NDC 坐标，再通过当前摄像机的视角 * 投影矩阵的逆矩阵来得到世界空间下的像素坐标，但是，这样的实现需要在片元着色器中进行矩阵乘法的操作，而这通常会影响游戏性能。我们将学习一个快速从深度纹理中重建世界坐标的方法。这种方法首先对图像空间下的视锥体射线（从摄像机出发，指向图像上的某点的射线）进行插值，这条射线存储了该像素在世界空间下到摄像机的方向信息。然后我们把该射线和线性化后的视角空间下的深度值相乘，再加上摄像机的世界位置，就可以得到该像素在世界空间下的位置。当我们得到世界坐标后，就可以轻松地使用各个公式来模拟全局雾效了。

重建世界坐标

在开始动手写代码之前，我们首先来了解如何从深度纹理中重建世界坐标。我们知道，坐标系中的一个顶点坐标可以通过它相对于另一个顶点坐标的偏移量来求得。重建像素的世界坐标也是基于这样的思想。我们只需要知道摄像机在世界空间下的位置，以及世界空间下该像素相对于摄像机的偏移量，把它们相加就可以得到该像素的世界坐标。整个过程可以使用下面的代码来表示：

1
float4 worldPos = _WorldSpaceCameraPos + linearDepth * interpolatedRay;

其中，_WorldSpaceCameraPos 是摄像机在世界空间下的位置，这可以由 Unity 的内置变量直接访问得到。而 linearDepth * interpolatedRay 则可以计算得到该像素相对于摄像机的偏移量，linearDepth 是由深度纹理得到的线性深度值，interpolatedRay 是由顶点着色器输出并插值后得到的射线，它不仅包含了该像素到摄像机的方向，也包含了距离信息。linearDepth 的获取我们已经详细解释过了，因此我们下面着重解释 interpolatedRay 的求法。

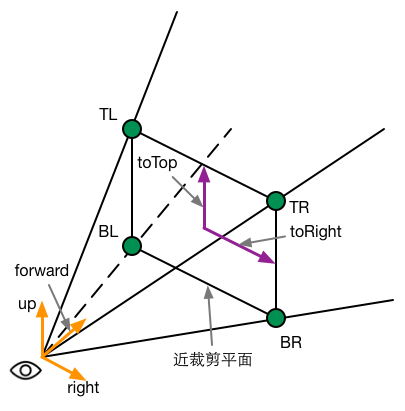
interpolatedRay 来源于对近裁剪平面的 4 个角的某个特定向量的插值，这 4 个向量包含了它们到摄像机的方向和距离信息，我们可以利用摄像机的近裁剪平面距离、FOV、纵横比计算而得。下图显示了计算时使用的一些辅助向量。

计算 interpolatedRay

为了方便计算，我们可以先计算两个向量——toTop 和 toRight，它们是起点位于近裁剪平面中心、分别指向摄像机正上方和正右方的向量。它们的计算公式如下：
$$
halfHeight = Near \times \tan{\frac{FOV}{2}}
$$
$$
toTop = camera.up \times halfHeight
$$
$$
toRight = camera.right \times halfHeight \cdot aspect
$$
其中，Near 是近裁剪平面的距离，FOV 是竖直方向的视角范围，camera.up、camera.right 分别对应了摄像机的正上方和正右方。

当得到这两个辅助向量后，我们就可以计算 4 个角相对于摄像机的方向了。我们以左上角为例（见上图中的 TL 点），它的计算公式如下：

$$
TL = camera.forward \cdot Near + toTop - toRight
$$

同理，其他 3 个角的计算也是类似的：
$$
TR = camera.forward \cdot Near + toTop + toRight
$$
$$
BL = camera.forward \cdot Near - toTop - toRight
$$
$$
BR = camera.forward \cdot Near - toTop + toRight
$$

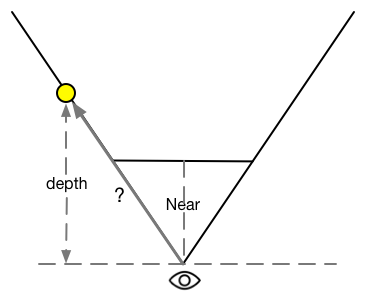
注意，上面求得的 4 个向量不仅包含了方向信息，它们的模对应了 4 个点打扫摄像机的空间距离。由于我们得到的线性深度值并非是点到摄像机的欧式距离，而是在 z 方向上的距离，因此，我们不能直接使用深度值和 4 个角的单位方向的乘积来计算它们到摄像机的偏移量，如下图所示。

采样得到的深度值并非是点到摄像机的欧式距离

想要把深度值转换成到摄像机的欧式距离也很简单，我们以 TL 点为例，根据相似三角形原理，TL 所在的射线上，像素的深度值和它到摄像机的实际距离的比等于近裁剪平面的距离和 TL 向量的模的比，即
$$
\frac{depth}{dist} = \frac{Near}{|TL|}
$$
由此可得，我们需要的 TL 距离摄像机的欧式距离 dist：
$$
dist = \frac{|TL|}{Near} \times depth
$$
由于 4 个点相互对称，因此其他 3 个向量的模和 TL 相等，即我们可以使用同一个因子和单位向量相乘，得到它们对应的向量值：
$$
scale = \frac{|TL|}{|Near|}
$$
$$
Ray_{TL} = \frac{TL}{|TL|} \times scale, Ray_{TR} = \frac{TR}{|TR|} \times scale
$$
$$
Ray_{BL} = \frac{BL}{|BL|} \times scale, Ray_{BR} = \frac{BR}{|BR|} \times scale
$$

屏幕后处理的原理是使用特定的材质去渲染一个刚好填充整个屏幕的四边形面片。这个四边形面片的 4 个顶点就对应了近裁剪平面的 4 个角。因此，我们可以把上面的计算结果传递给顶点着色器，顶点着色器根据当前的位置选择它所对应的向量，然后再将其输出，经插值后传递给片元着色器得到 interpolatedRay，我们就可以直接利用一开始提到的公式重建该像素在世界空间下的位置了。

雾的计算

在简单的雾效实现中，我们需要计算一个雾效系数 f，作为混合原始颜色和雾的颜色的混合系数：

1
float3 afterFog = f * fogColor + (1 - f) * origColor;

这个雾效系数 f 有很多计算方法。在 Unity 内置的雾效实现中，支持三种雾的计算方式——线性（Linear）、指数（Exponential）以及指数的平方（Exponential Squared）。当给定距离 z 后，f 的计算公式分别如下：

Linear：

$f = \frac{d_{max} - |z|}{d_{max} - d_{min}}$，$d_{min}$ 和 $d_{max}$ 分别表示受雾影响的最小距离和最大距离。

Exponential：

$f = e^{-d \cdot |z|}$，$d$ 是控制雾的浓度的参数。

Exponential Squared：

$f = e^{-(d - |z|)^2}$，$d$ 是控制雾的浓度的参数。

本次我们将使用类似线性雾的计算方式，计算基于高度的雾效。具体方法是，当给定一点在世界空间下的高度 y 后，f 的计算公式为：

$f = \frac{H_{end} - y}{H_{end} - H_{start}}$，$H_{start}$ 和 $H_{end}$ 分别表示受雾影响的起始高度和终止高度。

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
using UnityEngine;
using System.Collections;

public class FogWithDepthTexture : PostEffectsBase {

	public Shader fogShader;
	private Material fogMaterial = null;

	public Material material {  
		get {
			fogMaterial = CheckShaderAndCreateMaterial(fogShader, fogMaterial);
			return fogMaterial;
		}  
	}

	private Camera myCamera;
	public Camera camera {
		get {
			if (myCamera == null) {
				myCamera = GetComponent<Camera>();
			}
			return myCamera;
		}
	}

	private Transform myCameraTransform;
	public Transform cameraTransform {
		get {
			if (myCameraTransform == null) {
				myCameraTransform = camera.transform;
			}

			return myCameraTransform;
		}
	}

	[Range(0.0f, 3.0f)]
	public float fogDensity = 1.0f;

	public Color fogColor = Color.white;

	public float fogStart = 0.0f;
	public float fogEnd = 2.0f;

	void OnEnable() {
		camera.depthTextureMode |= DepthTextureMode.Depth;
	}
	
	void OnRenderImage (RenderTexture src, RenderTexture dest) {
		if (material != null) {
			Matrix4x4 frustumCorners = Matrix4x4.identity;

			float fov = camera.fieldOfView;
			float near = camera.nearClipPlane;
			float aspect = camera.aspect;

			float halfHeight = near * Mathf.Tan(fov * 0.5f * Mathf.Deg2Rad);
			Vector3 toRight = cameraTransform.right * halfHeight * aspect;
			Vector3 toTop = cameraTransform.up * halfHeight;

			Vector3 topLeft = cameraTransform.forward * near + toTop - toRight;
			float scale = topLeft.magnitude / near;

			topLeft.Normalize();
			topLeft *= scale;

			Vector3 topRight = cameraTransform.forward * near + toRight + toTop;
			topRight.Normalize();
			topRight *= scale;

			Vector3 bottomLeft = cameraTransform.forward * near - toTop - toRight;
			bottomLeft.Normalize();
			bottomLeft *= scale;

			Vector3 bottomRight = cameraTransform.forward * near + toRight - toTop;
			bottomRight.Normalize();
			bottomRight *= scale;

			frustumCorners.SetRow(0, bottomLeft);
			frustumCorners.SetRow(1, bottomRight);
			frustumCorners.SetRow(2, topRight);
			frustumCorners.SetRow(3, topLeft);

			material.SetMatrix("_FrustumCornersRay", frustumCorners);

			material.SetFloat("_FogDensity", fogDensity);
			material.SetColor("_FogColor", fogColor);
			material.SetFloat("_FogStart", fogStart);
			material.SetFloat("_FogEnd", fogEnd);

			Graphics.Blit (src, dest, material);
		} else {
			Graphics.Blit(src, dest);
		}
	}
}

fogDensity 用于控制雾的浓度，fogColor 用于控制雾的颜色。我们使用的雾效模拟函数是基于高度的，因此参数 fogStart 用于控制雾效的起始高度，fogEnd 用于控制雾效的终止高度。

OnRenderImage 首先计算了近裁剪平面的四个角对应的向量，并把它们存储在一个矩阵类型的变量（frustumCorners）中。计算过程我们已经详细解释过了，代码只是套用了之前讲过的公式而已。我们按一定顺序把这四个方向存储到了 frustumCorners 不同的行中，这个顺序是非常重要的，因为这决定了我们在顶点着色器中使用哪一行作为该点的待插值向量。随后，我们把结果和其他参数传递给材质，并调用 Graphics.Blit(src, dest, material) 把渲染结果显示在屏幕上。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
Shader "Custom/Chapter13/Chapter13-FogWithDepthTexture" {

    Properties {
        _MainTex ("Base (RGB)", 2D) = "white" {}
        _FogDensity ("Fog Density", Float) = 1.0
        _FogColor ("Fog Color", Color) = (1, 1, 1, 1)
        _FogStart ("Fog Start", Float) = 0.0
        _FogEnd ("Fog End", Float) = 1.0
    }

    SubShader {
        CGINCLUDE
        #include "UnityCG.cginc"

        float4x4 _FrustumCornersRay;

        sampler2D _MainTex;
        half4 _MainTex_TexelSize;
        sampler2D _CameraDepthTexture;
        half _FogDensity;
        fixed4 _FogColor;
        float _FogStart;
        float _FogEnd;

       

        struct v2f {
            float4 pos : SV_POSITION;
            half2 uv : TEXCOORD0;
            half2 uv_depth : TEXCOORD1;
            float4 interpolatedRay : TEXCOORD2;
        };

        v2f vert(appdata_img v) {
            v2f o;
            o.pos = UnityObjectToClipPos(v.vertex);
            o.uv = v.texcoord;
            o.uv_depth = v.texcoord;

            #if UNITY_UV_STARTS_AT_TOP
            if(_MainTex_TexelSize.y < 0)
                o.uv_depth.y = 1 - o.uv_depth.y;
            #endif

            int index = 0;
            if (v.texcoord.x < 0.5 && v.texcoord.y < 0.5) {
                index = 0;
            } else if (v.texcoord.x > 0.5 && v.texcoord.y < 0.5) {
                index = 1;
            } else if (v.texcoord.x > 0.5 && v.texcoord.y > 0.5) {
                index = 2;
            } else {
                index = 3;
            }

            #if UNITY_UV_STARTS_AT_TOP
            if(_MainTex_TexelSize.y < 0)
                index = 3 - index;
            #endif

            o.interpolatedRay = _FrustumCornersRay[index];
            return o;
        }

        fixed4 frag(v2f i) : SV_Target {
            float linearDepth = LinearEyeDepth(SAMPLE_DEPTH_TEXTURE(_CameraDepthTexture, i.uv_depth));
            float3 worldPos = _WorldSpaceCameraPos + linearDepth * i.interpolatedRay.xyz;

            float fogDensity = (_FogEnd - worldPos.y) / (_FogEnd - _FogStart);
            fogDensity = saturate(fogDensity * _FogDensity);

            fixed4 finalColor = tex2D(_MainTex, i.uv);
            finalColor.rgb = lerp(finalColor.rgb, _FogColor.rgb, fogDensity);

            return finalColor;
        }
        ENDCG

        Pass {
            ZTest Always Cull Off ZWrite Off
            CGPROGRAM
            #pragma vertex vert
            #pragma fragment frag
            ENDCG
        }
    }

    FallBack Off
}

在 v2f 结构体中，我们除了定义顶点位置、屏幕图像和深度纹理的纹理坐标外，还定义了 interpolatedRay 变量存储插值后的像素向量。在顶点着色器中，我们对深度纹理的采样坐标进行了平台差异化除了。更重要的是，我们要决定该点对应了 4 个角中的哪个角。我们采用的方法是判断它的纹理坐标。我们知道，在 Unity 中，纹理坐标的(0, 0)点对应了左下角，而(1, 1)点对应了右上角。我们据此来判断该顶点对应的索引，这个对应关系和我们在脚本中对 frustumCorners 的赋值顺序是一致的。实际上，不同平台的纹理坐标不一定是满足上面的条件的，例如 DirectX 和 Metal 这样的平台，左上角对应了(0, 0)点，但大多数情况下 Unity 会把这些平台下的屏幕图像进行翻转，因此我们仍然可以利用这个条件。但如果在类似 DirectX 的平台上开启了抗锯齿，Unity 就不会进行这个翻转。为了此时仍然可以得到相应顶点位置的索引值，我们对索引值也进行了平台差异化处理，以便在必要时也对索引值进行翻转。最后，我们使用索引值来获取 _FrustumCornersRay 中对应的行作为该顶点的 interpolatedRay 值。

首先我们需要重建该像素在世界空间中的位置。为此，我们首先使用 SAMPLE_DEPTH_TEXTURE 对深度纹理进行采样，再使用 LinearEyeDepth 得到视角空间下的线性深度值。之后，与 interpolatedRay 相乘后再和世界空间下的摄像机位置相加，即可得到世界空间下的位置。

得到世界坐标后，模拟雾效就变得非常容易。在本例中，我们选择实现基于高度的雾效模拟，我们根据材质属性 _FogEnd 和 _FogStart 计算当前的像素高度 worldPos.y 对应的雾效系数 fogDensity，再和参数 _FogDensity 相乘后，利用 saturate 函数截取到[0, 1]范围内，作为最后的雾效系数。然后，我们使用该系数将雾的颜色和原始颜色进行混合后返回。

再谈边缘检测

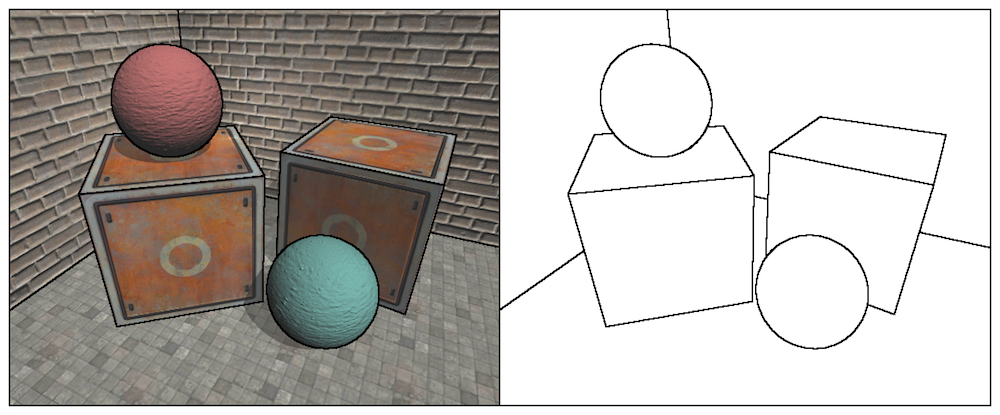
我们曾介绍如何使用 Sobel 算子对屏幕图像进行边缘检测，实现描边的效果。但是，这种直接利用颜色信息进行边缘检测的方法会产生很多我们不希望得到的边缘线，如下图所示；

直接对颜色图像进行边缘检测的结果

可以看出，物体的纹理、阴影等位置也被描上黑边，而这往往不是我们希望看到的。我们将学习如何在深度和法线纹理上进行边缘检测，这些图像不会受纹理和光照的影响，而仅仅保存了当前渲染物体的模型信息，通过这样的方式检测出来的边缘更加可靠。我们将实现类似下图中的效果。

在深度和法线纹理上进行更健壮的边缘检测

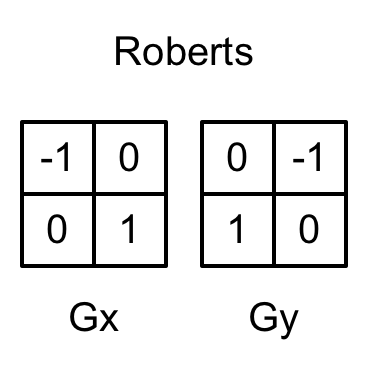
与使用 Sobel 算子不同，我们将使用 Roberts 算子来进行边缘检测。它使用的卷积核如下图所示。

Roberts算子

Roberts 算子的本质就是计算左上角和右下角的差值，乘以右上角和左下角的差值，作为评估边缘的依据。在下面的实现中，我们也会按这样的方式，取对角方向的深度或法线值，比较它们之间的插值，如果超过某个阈值（可由参数控制），就认为它们之间存在一条边。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
using UnityEngine;
using System.Collections;

public class EdgeDetectNormalsAndDepth : PostEffectsBase {

	public Shader edgeDetectShader;
	private Material edgeDetectMaterial = null;
	public Material material {  
		get {
			edgeDetectMaterial = CheckShaderAndCreateMaterial(edgeDetectShader, edgeDetectMaterial);
			return edgeDetectMaterial;
		}  
	}

	[Range(0.0f, 1.0f)]
	public float edgesOnly = 0.0f;

	public Color edgeColor = Color.black;

	public Color backgroundColor = Color.white;

	public float sampleDistance = 1.0f;

	public float sensitivityDepth = 1.0f;

	public float sensitivityNormals = 1.0f;
	
	void OnEnable() {
		GetComponent<Camera>().depthTextureMode |= DepthTextureMode.DepthNormals;
	}

	[ImageEffectOpaque]
	void OnRenderImage (RenderTexture src, RenderTexture dest) {
		if (material != null) {
			material.SetFloat("_EdgeOnly", edgesOnly);
			material.SetColor("_EdgeColor", edgeColor);
			material.SetColor("_BackgroundColor", backgroundColor);
			material.SetFloat("_SampleDistance", sampleDistance);
			material.SetVector("_Sensitivity", new Vector4(sensitivityNormals, sensitivityDepth, 0.0f, 0.0f));

			Graphics.Blit(src, dest, material);
		} else {
			Graphics.Blit(src, dest);
		}
	}
}

sampleDistance 用于控制对深度+法线纹理采样时，使用的采样距离。从视觉上看，sampleDistance 值越大，描边越宽。sensitivityDepth 和 sensitivityNormals 将会影响当邻域的深度值或法线值相差多少时，会被认为存在一条边界。如果把灵敏度调得很大，那么可能即使是深度或法线上很小的变化也会形成一条边。

需要注意的是，这里我们为 OnRenderImage 函数添加了[ImageEffectOpaque]属性。在默认情况下，OnRenderImage 函数会在所有的不透明和透明的 Pass 执行完毕后被调用，以便对场景中所有游戏对象都产生影响。但有时，我们希望在不透明的 Pass（即渲染队列小于等于 2500 的 Pass，内置的 Background、Geometry 和 AlphaTest 渲染队列均在此范围内）执行完毕后立即调用该函数，而不对透明物体（渲染队列为 Transparent 的 Pass）产生影响，此时，我们可以在 OnRenderImage 函数前添加 ImageEffectOpaque 属性来实现这样的目的。在本例中，我们只希望对不透明物体进行描边，而不希望透明物体也被描边，因此需要添加该属性。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
Shader "Custom/Chapter13/Chapter13-EdgeDetectNormalAndDepth" {

    Properties {
        _MainTex ("Base (RGB)", 2D) = "white" {}
        _EdgeOnly ("Edge Only", Float) = 1.0
        _EdgeColor ("Edge Color", Color) = (0, 0, 0, 1)
        _BackgroundColor ("Background Color", Color) = (1, 1, 1, 1)
        _SampleDistance ("Sample Distance", Float) = 1.0
        _Sensitivity ("Sensitivity", Vector) = (1, 1, 1, 1)
    }

    SubShader {
        CGINCLUDE
        #include "UnityCG.cginc"

        sampler2D _MainTex;
        half4 _MainTex_TexelSize;
        fixed _EdgeOnly;
        fixed4 _EdgeColor;
        fixed4 _BackgroundColor;
        float _SampleDistance;
        half4 _Sensitivity;
        sampler2D _CameraDepthNormalsTexture;

        struct v2f {
            float4 pos : SV_POSITION;
            half2 uv[5] : TEXCOORD0;
        };

        v2f vert(appdata_img v) {
            v2f o;
            o.pos = UnityObjectToClipPos(v.vertex);

            half2 uv = v.texcoord;
            o.uv[0] = uv;

            #if UNITY_UV_STARTS_AT_TOP
            if (_MainTex_TexelSize.y < 0)
            uv.y = 1 - uv.y;
            #endif

            o.uv[1] = uv + _MainTex_TexelSize.xy * half2(1, 1) * _SampleDistance;
            o.uv[2] = uv + _MainTex_TexelSize.xy * half2(-1, -1) * _SampleDistance;
            o.uv[3] = uv + _MainTex_TexelSize.xy * half2(-1, 1) * _SampleDistance;
            o.uv[4] = uv + _MainTex_TexelSize.xy * half2(1, -1) * _SampleDistance;
            return o;
        }


        half CheckSame(half4 center, half4 sample) {
            half2 centerNormal = center.xy;
            float centerDepth = DecodeFloatRG(center.zw);
            half2 sampleNormal = sample.xy;
            float sampleDepth = DecodeFloatRG(sample.zw);

            //difference in normals
            //do not bother decoding normal - there's no need here
            half2 diffNormal = abs(centerNormal - sampleNormal) * _Sensitivity.x;
            int isSameNormal = (diffNormal.x + diffNormal.y) < 0.1;
            //difference in depth
            float diffDepth  = abs(centerDepth - sampleDepth) * _Sensitivity.y;
            //scale the required threshold by the distance
            int isSameDepth = diffDepth < 0.1 * centerDepth;

            //return:
            //1 - if normals and depth are similar enough
            //0 - otherwise
            return isSameNormal * isSameDepth ? 1.0 : 0.0;
        }

        fixed4 fragRobertsCrossDepthAndNormal(v2f i) : SV_Target {
            half4 sample1 = tex2D(_CameraDepthNormalsTexture, i.uv[1]);
            half4 sample2 = tex2D(_CameraDepthNormalsTexture, i.uv[2]);
            half4 sample3 = tex2D(_CameraDepthNormalsTexture, i.uv[3]);
            half4 sample4 = tex2D(_CameraDepthNormalsTexture, i.uv[4]);

            half edge = 1.0;
            edge *= CheckSame(sample1, sample2);
            edge *= CheckSame(sample3, sample4);

            fixed4 withEdgeColor = lerp(_EdgeColor, tex2D(_MainTex, i.uv[0]), edge);
            fixed4 onlyEdgeColor = lerp(_EdgeColor, _BackgroundColor, edge);

            return lerp(withEdgeColor, onlyEdgeColor, _EdgeOnly); 
        }
        ENDCG

        Pass {
            ZTest Always Cull Off ZWrite Off
            CGPROGRAM
            #pragma vertex vert
            #pragma fragment fragRobertsCrossDepthAndNormal
            ENDCG
        }
    }

    FallBack Off
}

_Sensitivity 的 xy 分量分别对应了法线和深度的检测灵敏度，zw分量则没有实际用途。我们在 v2f 结构体中定义了一个维数为 5 的纹理坐标数组。这个数组的第一个坐标存储了屏幕颜色图像的采样纹理。我们对深度纹理的采样坐标进行了平台差异化处理，在必要情况下对它的竖直方向进行了翻转。数组中剩余的 4 个坐标则存储了使用 Roberts 算子时需要采样的纹理坐标，我们还使用了 _SampleDistance 来控制采样距离。通过把计算采样纹理坐标的代码从片元着色器中转移到顶点着色器中，可以减少运算，提高性能。由于从顶点着色器到片元着色器的插值是线性的，因此这样的转移并不会影响纹理坐标的计算结果。

在片元着色器中我们首先使用 4 个纹理坐标对深度+法线纹理进行采样，再调用 CheckSame 函数来分别计算对角线上两个纹理值的插值。CheckSame 函数的返回值要么是 0，要么是 1，返回 0 时表明这两点之间存在一条边界，反之则返回 1。

CheckSame 首先对输入参数进行处理，得到两个采样点的法线和深度值。值得注意的是，这里我们并没有解码得到真正的法线值，而是直接使用了 xy 分量。这是因为我们只需要比较两个采样值之间的差异度，而并不需要知道它们真正的法线值。然后，我们把两个采样点的对应值相减并取绝对值，再乘以灵敏度参数，把差异值的每个分量相加再和一个阈值比较，如果它们的和小于阈值，则返回 1，说明差异不明显，不存在一条边界；否则返回 0。最后，我们把法线和深度的检查结果相乘，作为组合后的返回值。当通过 CheckSame 函数得到边缘信息后，片元着色器就利用该值进行颜色混合。

本次实现的描边效果是基于整个屏幕空间进行的，也就是说，场景内的所有物体都会被添加描边效果。但有时，我们希望只对特定的物体进行描边，例如当玩家选中场景中的某个物体后，我们想要在该物体周围添加一层描边效果。这时，我们可以使用 Unity 提供的 Graphics.DrawMesh 或 Graphics.DrawMeshNow 函数把需要描边的物体再次渲染一遍（在所有不透明物体渲染完毕之后），然后再使用本节提到的边缘检测算法计算深度或法线纹理中每个像素的梯度值，判断它们是否小于某个阈值，如果是，就在 Shader 中使用 clip() 函数将该像素剔除掉，从而显示出原来的物体颜色。

Unity Shader
#Texture
深度和法线纹理
http://example.com/posts/深度和法线纹理/
作者
祭零小白
发布于
2022年3月21日
许可协议