本文最后更新于:2025年4月17日 晚上
线性插值函数
l e r p ( y 1 , y 2 , w e i g h t ) = y 1 + ( y 2 − y 1 ) × w e i g h t lerp(y_1, y_2, weight) = y_1 + (y_2 - y_1) \times weight
l er p ( y 1 , y 2 , w e i g h t ) = y 1 + ( y 2 − y 1 ) × w e i g h t
其中 w e i g h t weight w e i g h t w e i g h t weight w e i g h t
这里 y 1 y_1 y 1 y 2 y_2 y 2 y 1 y_1 y 1 y 2 y_2 y 2 w e i g h t weight w e i g h t w e i g h t weight w e i g h t
l e r p ( y 1 , y 2 , w e i g h t ) = ( 1 − w e i g h t ) × y 1 + w e i g h t × y 2 lerp(y_1, y_2, weight) = (1 - weight) \times y_1 + weight \times y_2
l er p ( y 1 , y 2 , w e i g h t ) = ( 1 − w e i g h t ) × y 1 + w e i g h t × y 2
简单来说,lerp 函数是在 y 1 y_1 y 1 y 2 y_2 y 2 y 1 y_1 y 1 y 2 y_2 y 2
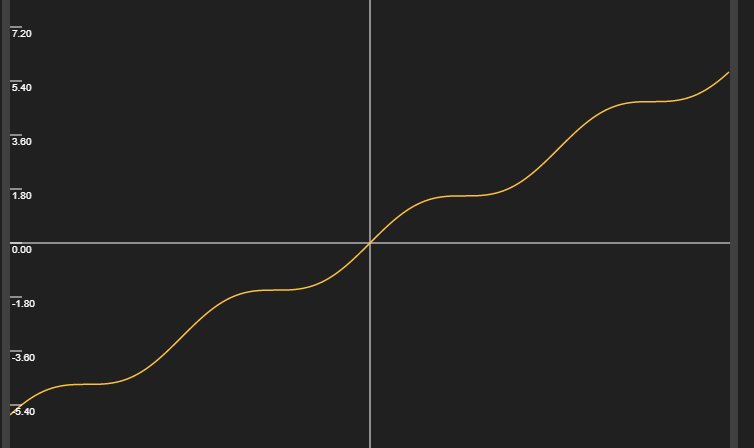
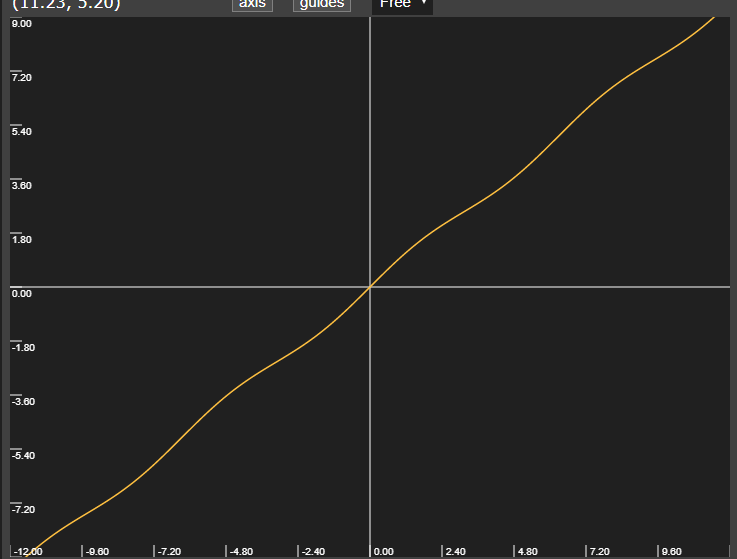
再看一下最简单的线性函数 y = x y = x y = x
在它俩之间过渡,我们只需要使用 l e r p ( sin x , x , 0.5 ) lerp(\sin x, x, 0.5) l er p ( sin x , x , 0.5 ) w e i g h t weight w e i g h t
当 y 1 y_1 y 1 y 2 y_2 y 2
贝塞尔曲线
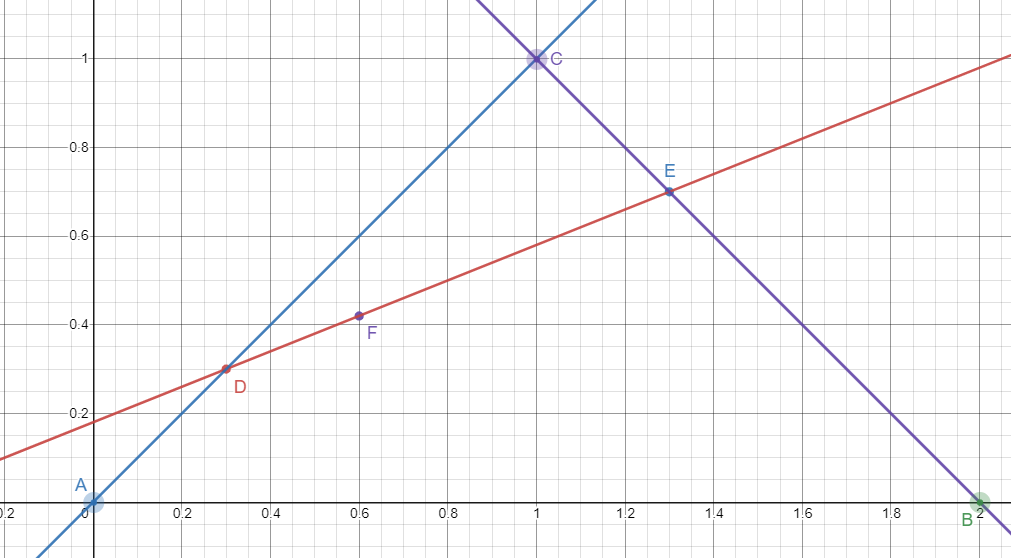
当有 A A A B B B C C C D D D A A A C C C t t t E E E C C C B B B t t t F F F D D D E E E t t t F F F A A A B B B C C C
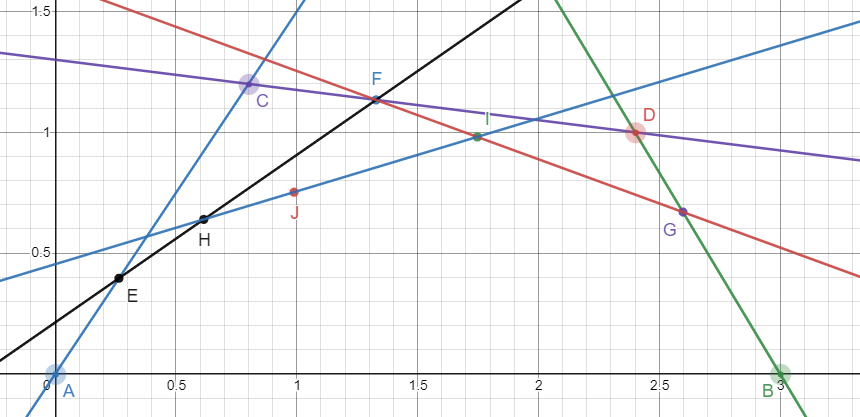
同理,当有 A A A B B B C C C D D D E E E A A A C C C t t t F F F C C C D D D t t t G G G D D D B B B t t t H H H E E E F F F t t t I I I F F F G G G t t t J J J H H H I I I t t t J J J A A A B B B C C C D D D
二阶贝塞尔曲线公式推导
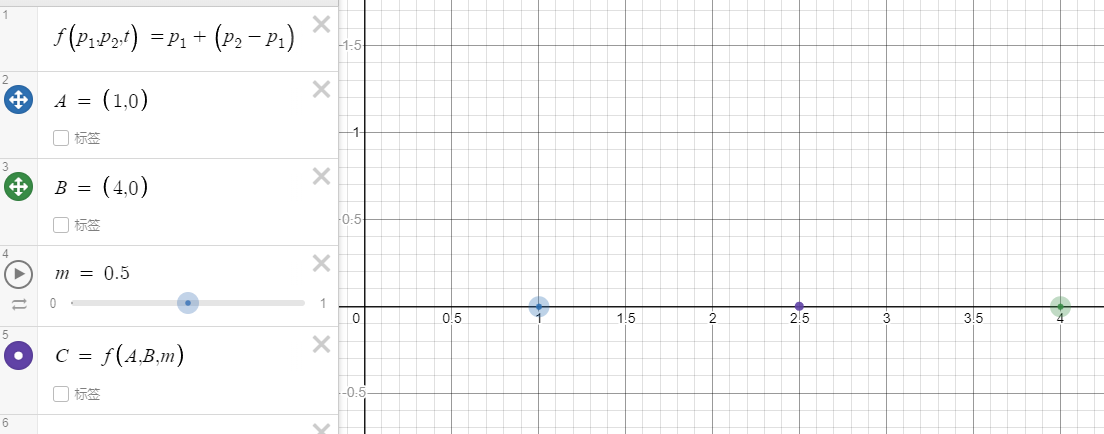
由 f ( p 0 , p 1 , t ) = ( p 1 − p 0 ) × t + p 0 f(p_0, p_1, t) = (p_1 - p_0) \times t + p_0 f ( p 0 , p 1 , t ) = ( p 1 − p 0 ) × t + p 0
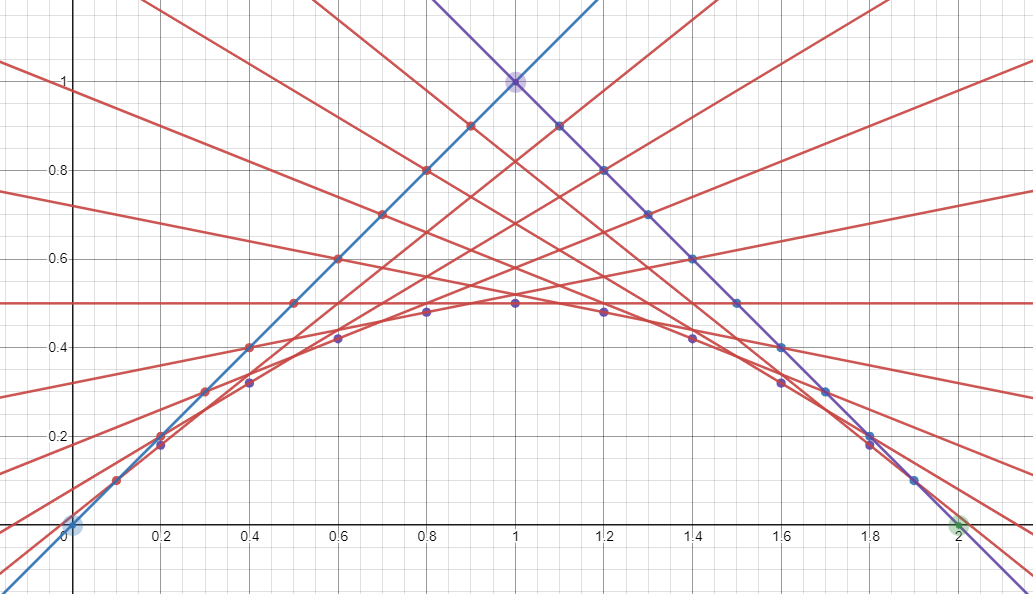
D = ( C − A ) t + A E = ( B − C ) t + C F = ( E − D ) t + D = ( ( ( B − C ) t + C ) − ( ( C − A ) t + A ) t + ( ( C − A ) t + A ) ) = ( A t + B t − 2 C t + C − A ) t + C t − A t + A = ( t − 1 ) 2 A + t 2 B + 2 t ( 1 − t ) C B ( t ) = ( 1 − t ) 2 A + t 2 B + 2 t ( 1 − t ) C , t ∈ [ 0 , 1 ] \begin{aligned}
D &= (C - A)t + A\\
E &= (B - C)t + C\\
F &= (E - D)t + D\\
&= (((B - C)t + C) - ((C - A)t + A)t + ((C - A)t + A))\\
&= (At + Bt -2Ct + C - A)t + Ct - At + A\\
&= (t - 1)^2A + t^2B + 2t(1 - t)C\\
\\
B(t) &= (1 - t)^2A + t^2B + 2t(1 - t)C, t \in [0, 1]
\end{aligned}
D E F B ( t ) = ( C − A ) t + A = ( B − C ) t + C = ( E − D ) t + D = ((( B − C ) t + C ) − (( C − A ) t + A ) t + (( C − A ) t + A )) = ( A t + Bt − 2 Ct + C − A ) t + Ct − A t + A = ( t − 1 ) 2 A + t 2 B + 2 t ( 1 − t ) C = ( 1 − t ) 2 A + t 2 B + 2 t ( 1 − t ) C , t ∈ [ 0 , 1 ]
三阶贝塞尔曲线公式推导
由 f ( p 0 , p 1 , t ) = ( p 1 − p 0 ) × t + p 0 f(p_0, p_1, t) = (p_1 - p_0) \times t + p_0 f ( p 0 , p 1 , t ) = ( p 1 − p 0 ) × t + p 0
E = ( C − A ) t + A F = ( D − C ) t + C G = ( B − D ) t + D \begin{aligned}
E &= (C - A)t + A\\
F &= (D - C)t + C\\
G &= (B - D)t + D\\
\end{aligned}
E F G = ( C − A ) t + A = ( D − C ) t + C = ( B − D ) t + D
H H H A A A D D D C C C I I I C C C B B B D D D
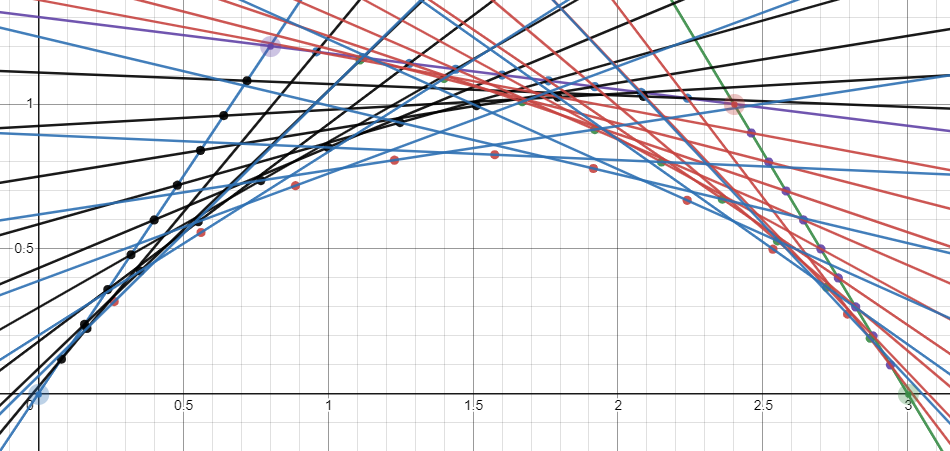
H = ( F − E ) t + E = ( 1 − t ) 2 A + t 2 D + 2 t ( 1 − t ) C I = ( G − F ) t + F = ( 1 − t ) 2 C + t 2 B + 2 t ( 1 − t ) D J = ( I − H ) t + H = ( ( ( 1 − t ) 2 C + t 2 B + 2 t ( 1 − t ) D ) − ( ( 1 − t ) 2 A + t 2 D + 2 t ( 1 − t ) C ) ) t + ( ( 1 − t ) 2 A + t 2 D + 2 t ( 1 − t ) C ) = ( 1 − t ) 3 A + t 3 B + 3 t ( 1 − t ) 2 C + 3 t 2 ( 1 − t ) D B ( t ) = ( 1 − t ) 3 A + t 3 B + 3 t ( 1 − t ) 2 C + 3 t 2 ( 1 − t ) D , t ∈ [ 0 , 1 ] \begin{aligned}
H &= (F - E)t + E\\
&= (1 - t)^2A + t^2D + 2t(1 - t)C\\
\\
I &= (G - F)t + F\\
&= (1 - t)^2C + t^2B + 2t(1 - t)D\\
\\
J &= (I - H)t + H\\
&= (((1 - t)^2C + t^2B + 2t(1 - t)D) - ((1 - t)^2A + t^2D + 2t(1 - t)C))t + ((1 - t)^2A + t^2D + 2t(1 - t)C)\\
&= (1 - t)^3A + t^3B + 3t(1 - t)^2C + 3t^2(1 - t)D\\
\\
B(t) &= (1 - t)^3A + t^3B + 3t(1 - t)^2C + 3t^2(1 - t)D, t \in [0, 1]
\end{aligned}
H I J B ( t ) = ( F − E ) t + E = ( 1 − t ) 2 A + t 2 D + 2 t ( 1 − t ) C = ( G − F ) t + F = ( 1 − t ) 2 C + t 2 B + 2 t ( 1 − t ) D = ( I − H ) t + H = ((( 1 − t ) 2 C + t 2 B + 2 t ( 1 − t ) D ) − (( 1 − t ) 2 A + t 2 D + 2 t ( 1 − t ) C )) t + (( 1 − t ) 2 A + t 2 D + 2 t ( 1 − t ) C ) = ( 1 − t ) 3 A + t 3 B + 3 t ( 1 − t ) 2 C + 3 t 2 ( 1 − t ) D = ( 1 − t ) 3 A + t 3 B + 3 t ( 1 − t ) 2 C + 3 t 2 ( 1 − t ) D , t ∈ [ 0 , 1 ]
或者 J J J E E E G G G F F F
E = ( C − A ) t + A F = ( D − C ) t + C G = ( B − D ) t + D J = ( 1 − t ) 2 E + t 2 G + 2 t ( 1 − t ) F = ( 1 − t ) 2 ( ( C − A ) t + A ) + t 2 ( ( B − D ) t + D ) + 2 t ( 1 − t ) ( ( D − C ) t + C ) = ( 1 − t ) 3 A + t 3 B + 3 t ( 1 − t ) 2 C + 3 t 2 ( 1 − t ) D B ( t ) = ( 1 − t ) 3 A + t 3 B + 3 t ( 1 − t ) 2 C + 3 t 2 ( 1 − t ) D , t ∈ [ 0 , 1 ] \begin{aligned}
E &= (C - A)t + A\\
F &= (D - C)t + C\\
G &= (B - D)t + D\\
J &= (1 - t)^2E + t^2G + 2t(1 - t)F\\
&= (1 - t)^2((C - A)t + A) + t^2((B - D)t + D) + 2t(1 - t)((D - C)t + C)\\
&= (1 - t)^3A + t^3B + 3t(1 - t)^2C + 3t^2(1 - t)D\\
\\
B(t) &= (1 - t)^3A + t^3B + 3t(1 - t)^2C + 3t^2(1 - t)D, t \in [0, 1]
\end{aligned}
E F G J B ( t ) = ( C − A ) t + A = ( D − C ) t + C = ( B − D ) t + D = ( 1 − t ) 2 E + t 2 G + 2 t ( 1 − t ) F = ( 1 − t ) 2 (( C − A ) t + A ) + t 2 (( B − D ) t + D ) + 2 t ( 1 − t ) (( D − C ) t + C ) = ( 1 − t ) 3 A + t 3 B + 3 t ( 1 − t ) 2 C + 3 t 2 ( 1 − t ) D = ( 1 − t ) 3 A + t 3 B + 3 t ( 1 − t ) 2 C + 3 t 2 ( 1 − t ) D , t ∈ [ 0 , 1 ]
阶梯插值函数
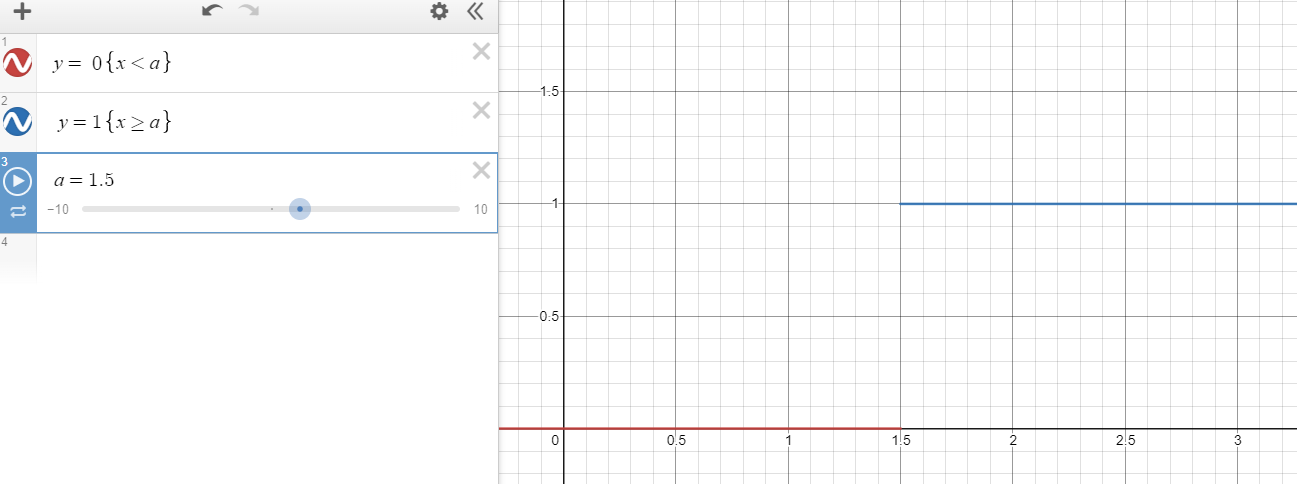
step 函数的逻辑是
1 2 3 4 5 6 step(a, x){
平滑阶梯插值函数
smoothstep 函数可以用来生成 0 到 1 的平滑过渡值,它也叫平滑阶梯函数。smoothstep 函数的定义是
1 2 3 4 5 float smoothstep(float a, float b, float x)
简单来说就是:
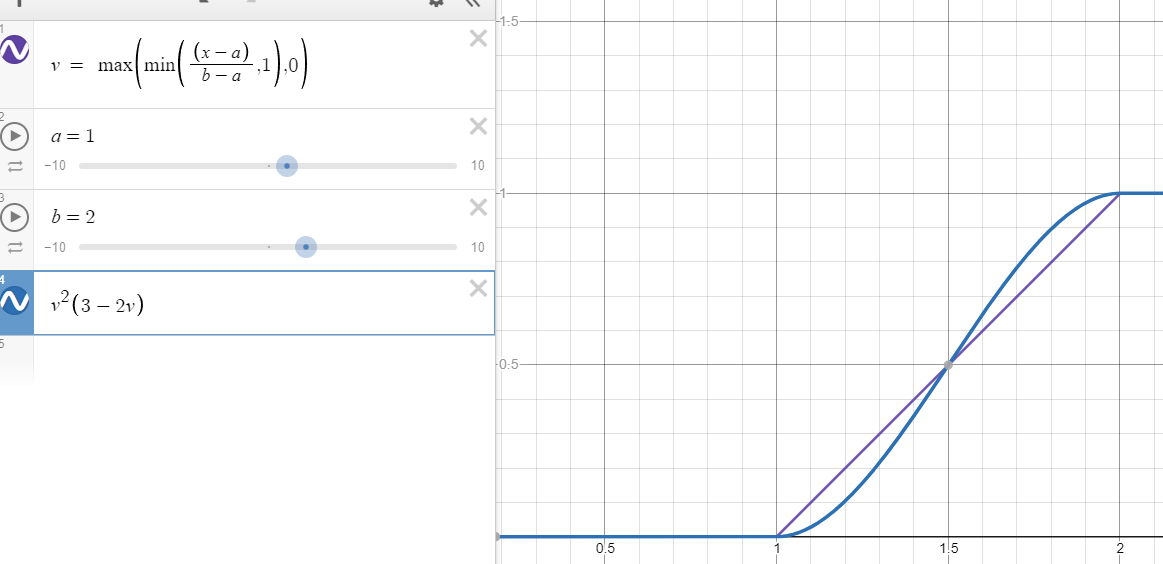
在 a < b 的情况下,当 x < a 时,返回 0,当 x > b 时,返回 1,否则在 0 和 1 之间平滑过渡:
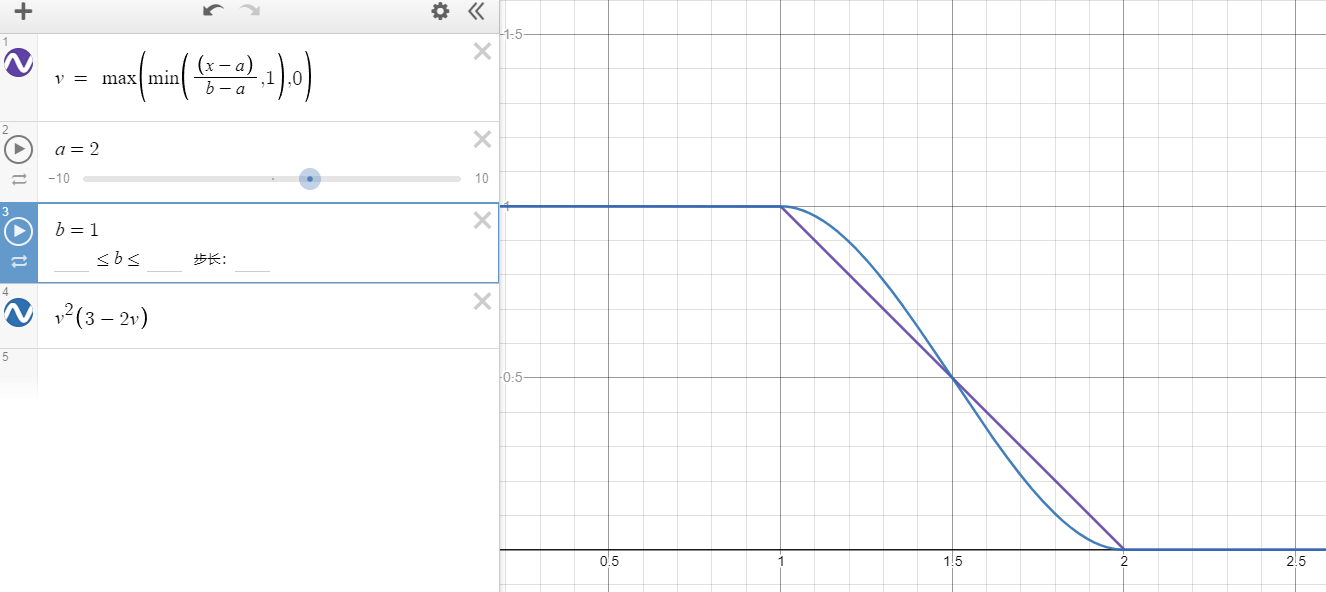
在 a > b 的情况下,当 x < b 时,返回 1,当 x > a 时,返回 0,否则在 0 和 1 之间平滑过渡:
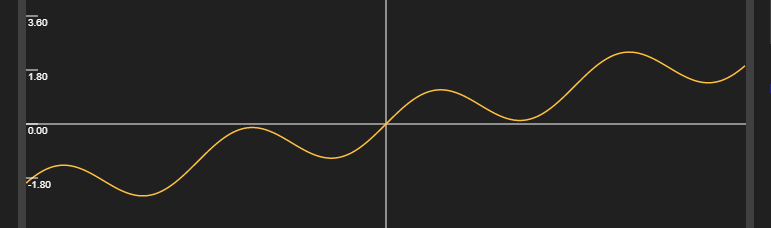
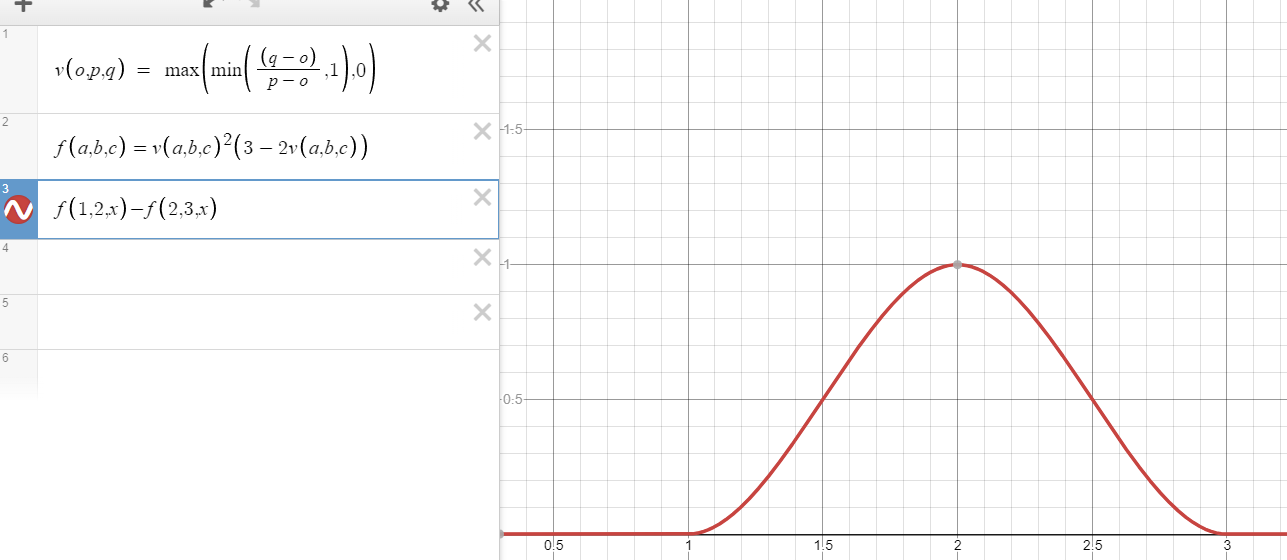
两个 smoothstep 进行减法运算可以得到一些波形图,例如 smoothstep(1, 2, x) - smoothstep(2, 3, x):
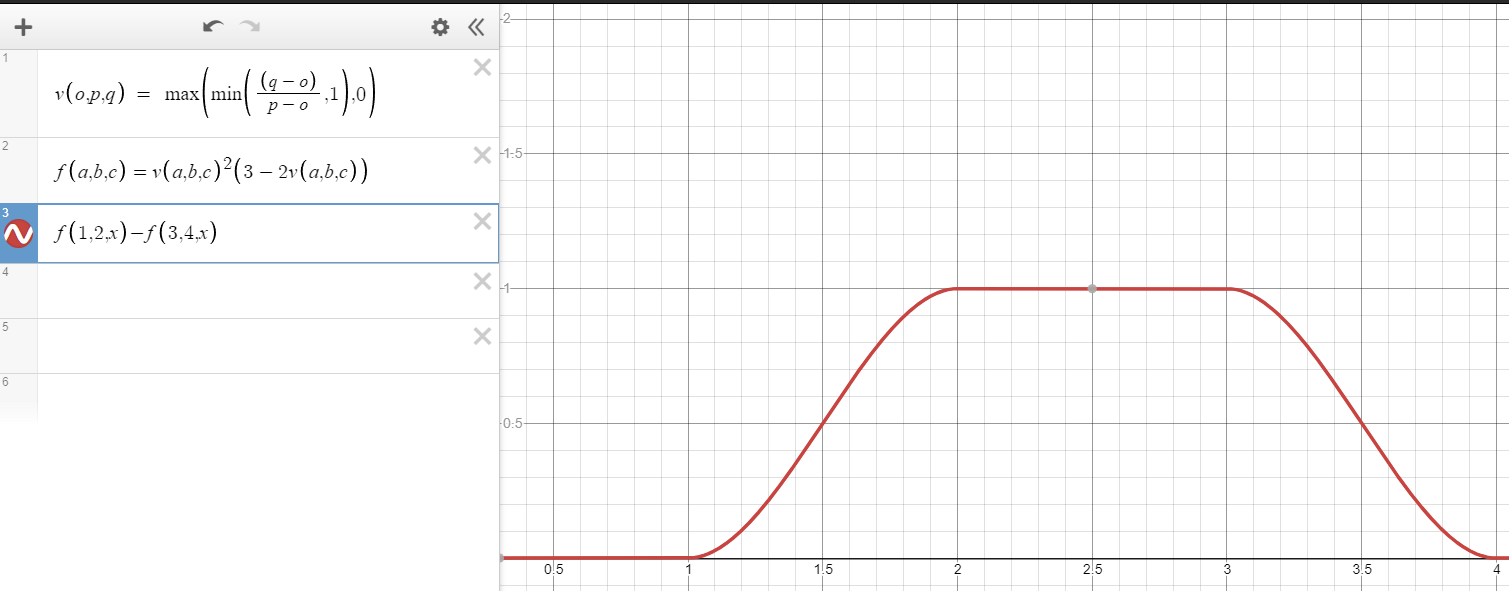
想要增加波峰的持续宽度,可以构造 smoothstep(1, 2, x) - smoothstep(3, 4, x):