四元数和三维旋转(二)

四元数

所有的四元数 $q \in \mathbb{H}$ 都可以写成下面这种形式：
$$
q = a + bi + cj + dk,(a,b,c,d \in \mathbb{R})
$$

其中
$$
i^2 = j^2 = k^2 = ijk = -1
$$

如果把上式称为四元数的代数形式，那么和复数类似，它也有对应的向量形式一：
$$
q = \begin{bmatrix}
a\ b\ c\ d\
\end{bmatrix}
$$

如果将四元数 $q$ 的实部和虚部分开，并用一个三维的向量来表示虚部，将它表示为标量和向量的有序对形式，那么四元数还可以表示为下述的向量形式二：
$$
q = [s, \pmb{v}], (\pmb{v} = \begin{bmatrix} x\ y\ z\ \end{bmatrix},\quad s,x,y,z \in \mathbb{R})
$$

四元数的性质

四元数的模长

仿照复数模长的定义，我们可以暂时将四元数 $q = a + bi + cj + dk$ 的模长定义为
$$
\lVert q \rVert = \sqrt{a^2 + b^2 + c^2 + d^2}
$$
如果用标量向量有序对的形式进行表示的话，$q = [s, \pmb{v}]$ 的模长为：
$$
\lVert q \rVert = \sqrt{s^2 + \lVert\pmb{v}\rVert^2} = \sqrt{s^2 + \pmb{v}\cdot\pmb{v}}
$$

四元数的加减法

与复数类似，四元数的加法只需要将分量相加就可以了，如果我们有两个四元数 $q_{1} = a + bi + cj + dk$，$q_{2} = e + fi + gj + hk$，那么它们的和为
$$
\begin{aligned}
q_{1} + q_{2} &= a + bi + cj + dk + e + fi + gj + hk\
&= (a + e) + (b + f)i + (c + g)j + (d + h)k
\end{aligned}
$$

减法同理，将加号改为减号就可以了
$$
q_{1} - q_{2} = (a - e) + (b - f)i + (c - g)j + (d - h)k
$$

如果四元数是以标量向量有序对形式定义的，比如说 $q_{1} = [s, \pmb{v}]$，$q_{2} = [t, \pmb{u}]$，那么
$$
q_{1} \pm q_{2} = [s \pm t, \pmb{v}\pm\pmb{u}]
$$

四元数的标量乘法

如果我们有一个四元数 $q = a + bi + cj + dk$ 和一个标量 $s$，那么它们的乘积为：
$$
\begin{aligned}
sq &= s(a + bi + cj + dk)\
&= sa + sbi + scj + sdk
\end{aligned}
$$

四元数与标量的乘法遵守交换律，也就是说 $sq = qs$

四元数乘法

四元数之间的乘法不遵守交换律，也就是说一般情况下 $q_{1}q_{2} \neq q_{2}q_{1}$。这也就有了左乘和右乘的区别，如果是 $q_{1}q_{2}$，我们就说"$q_{2}$ 左乘以 $q_{1}$“，如果是 $q_{2}q_{1}$，那我们就说”$q_{2}$ 右乘以 $q_{1}$"。除了交换律之外，结合律和分配律在四元数内都是成立的。

如果有两个四元数 $q_{1} = a + bi + cj + dk$ 和 $q_{2} = e + fi + gj + hk$，那么
$$
\begin{aligned}
q_{1}q_{2} &= (a + bi + cj + dk)(e + fi + gj + hk)\
&= ae + afi + agj + ahk +\
&\quad bei + bfi^2 + bgij + bhik +\
&\quad cej + cfji + cgj^2 + chjk +\
&\quad dek + dfki + dgkj + dhk^2
\end{aligned}
$$

由 $i^2 = j^2 = k^2 = ijk = -1$ 我们可以推导出 $jk = i$，$ij = k$，$ki = j$，$kj = -i$，$ji = -k$，$ik = -j$，于是我们可以得到：

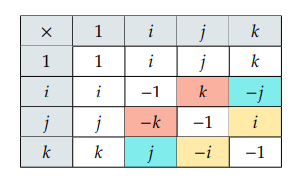
容易观察到交换律并不成立。利用上面的表格，我们可以对四元数之间的乘法进行归纳化简：
$$
\begin{aligned}
q_{1}q_{2}
&= ae + afi + agj + ahk +\
&\quad bei + bfi^2 + bgij + bhik +\
&\quad cej + cfji + cgj^2 + chjk +\
&\quad dek + dfki + dgkj + dhk^2\
&= (a\textcolor{red}{e} - b\textcolor{blue}{f} - c\textcolor{green}{g} - d\textcolor{orange}{h})+\
&\quad (b\textcolor{red}{e} + a\textcolor{blue}{f} - d\textcolor{green}{g} + c\textcolor{orange}{h})i+\
&\quad (c\textcolor{red}{e} + d\textcolor{blue}{f} + a\textcolor{green}{g} - b\textcolor{orange}{h})j+\
&\quad (d\textcolor{red}{e} - c\textcolor{blue}{f} + b\textcolor{green}{g} + a\textcolor{orange}{h})k\
\end{aligned}
$$

矩阵形式

可以看到，四元数的相乘其实也是一个线性组合，我们同样可以将它写成矩阵的形式：
$$
q_{1}q_{2} =
\begin{bmatrix}
a&-b&-c&-d\
b&a&-d&c\
c&d&a&-b\
d&-c&b&a\
\end{bmatrix}
\begin{bmatrix}
\textcolor{red}{e}\
\textcolor{blue}{f}\
\textcolor{green}{g}\
\textcolor{orange}{h}\
\end{bmatrix}
$$

注意，这个矩阵所作出的变换等价于左乘 $q_{1}$。因为四元数不符合乘法交换律，所以右乘 $q_{1}$的变换是一个不同的矩阵，它可以使用完全相同的方法推导而得，下面这个矩阵所作出的变换等价于右乘 $q_{1}$

$$
q_{2}q_{1} =
\begin{bmatrix}
a&-b&-c&-d\
b&a&d&-c\
c&-d&a&b\
d&c&-b&a\
\end{bmatrix}
\begin{bmatrix}
\textcolor{red}{e}\
\textcolor{blue}{f}\
\textcolor{green}{g}\
\textcolor{orange}{h}\
\end{bmatrix}
$$

Graßmann积

重新整理之前的乘法结果：

$$
\begin{aligned}
q_{1}q_{2} &= (ae -(bf + cg + dh))+\
&\quad(b\textcolor{red}{e} + \textcolor{blue}{a}f + ch - dg)i+\
&\quad(c\textcolor{red}{e} + \textcolor{blue}{a}g + df - bh)j+\
&\quad(d\textcolor{red}{e} + \textcolor{blue}{a}h + bg - cf)k\
\end{aligned}
$$

如果令 $\pmb{v} = \begin{bmatrix}b\ c\ d\ \end{bmatrix}$，$\pmb{u} = \begin{bmatrix}f\ g\ h\ \end{bmatrix}$，那么

$$
\pmb{v}\cdot\pmb{u} = bf + cg + dh
$$
$$
\begin{aligned}
\pmb{v}\times\pmb{u} &=
\begin{vmatrix}
\pmb{i}&\pmb{j}&\pmb{k}\
b&c&d\
f&g&h\
\end{vmatrix}\
&= (ch - dg)\pmb{i} - (bh - df)\pmb{j} + (bg - cf)\pmb{k}
\end{aligned}
$$

注意 $\pmb{v}\times\pmb{u}$ 的结果是一个向量，这里的 $\pmb{i}、\pmb{j}、\pmb{k}$ 是向量的基，如果使用标量向量有序对形式来表示，$q_{1}q_{2}$ 的结果可以用向量点乘和叉乘的形式表示出来

$$
q_{1}q_{2} = [ae - \pmb{v}\cdot\pmb{u}, a\pmb{u} + e\pmb{v} + \pmb{v}\times\pmb{u}]
$$

这个结果也被叫做 Graßmann积，一般来说：

Theorem 7：Graßmann积
对任意四元数 $q_{1} = [s, \pmb{v}]$，$q_{2} = [t, \pmb{u}]$，$q_{1}q_{2}$ 的结果是
$$
q_{1}q_{2} = [st - \pmb{v}\cdot\pmb{u}, s\pmb{u} + t\pmb{v} + \pmb{v}\times\pmb{u}]
$$

纯四元数

实部为零，仅有虚部的四元数为纯四元数，即：
$$
q = [0, \pmb{v}]
$$

对于两个纯四元数 $q_{1} = [0, \pmb{v}]$，$q_{2} = [0, \pmb{u}]$，那么它们的乘积为：
$$
q_{1}q_{2} = [-\pmb{v}\cdot\pmb{u}, \pmb{v}\times\pmb{u}]
$$

共轭

四元数 $q = a + bi + cj + dk$ 的共轭为 $q^* = a - bi - cj - dk$。如果用标量向量有序对的形式来定义的话，$q = [s, \pmb{v}]$ 的共轭为 $q^* = [s, -\pmb{v}]$。共轭四元数的一个非常有用的性质就是
$$
\begin{aligned}
qq^* &= [s, \pmb{v}]\cdot[s, -\pmb{v}]\
&= [s^2 - \pmb{v}\cdot(-\pmb{v}), s(-\pmb{v}) + s\pmb{v} + \pmb{v}\times(-\pmb{v})]\
&= [s^2 + \pmb{v}\cdot\pmb{v}, 0]\
&= s^2 + x^2 + y^2 + z^2\
&= \lVert q \rVert^2
\end{aligned}
$$
结果是一个标量，正是四元数模长的平方。
$$
q^q = (q^)(q^)^ = \lVert q^* \rVert^2 = \lVert q \rVert^2
$$
我们得到，$q^q = qq^$，这个特殊的乘法遵守交换律。

逆

因为四元数乘法不遵守交换律，我们不会将两个四元数相除写为 $\frac{p}{q}$ 的形式，取而代之的是将乘法的逆运算定义为 $pq^{-1}$ 或者 $q^{-1}p$，注意它们的结果一般是不同的。

其中，$q^{-1}$ 是 $q$ 的逆，我们规定
$$
qq^{-1} = q^{-1}q = 1\quad(q \neq 0)
$$

右乘 $q$ 的逆运算为右乘 $q^{-1}$，左乘 $q$ 的逆运算为左乘 $q^{-1}$。

利用共轭，我们可以进行如下推导：
$$
\begin{aligned}
qq^{-1} &= 1\
q^qq^{-1} &= q^\
\lVert q \rVert^2q^{-1} &= q^\
q^{-1} &= \frac{q^}{\lVert q \rVert^2}\
\end{aligned}
$$

四元数的逆就是它的共轭除以它模长的平方。如果 $\lVert q \rVert = 1$，那么它的逆就是它的共轭，此时称 $q$ 为一个单位四元数。

四元数与3D旋转

如果我们需要将一个向量 $\pmb{v}$ 沿着一个用单位向量所定义的旋转轴 $\pmb{u}$ 旋转 $\theta$ 度，那么我们可以将这个向量 $\pmb{v}$ 拆分为正交于旋转轴的 $\pmb{v_{\perp}}$ 以及平行于旋转轴的 $\pmb{v_{\parallel}}$。我们可以对这两个分向量分别进行旋转，获得 $\pmb{v_{\perp}‘}$ 和 $\pmb{v_{\parallel}’}$。将它们相加就是 $\pmb{v}$ 旋转之后的结果 $\pmb{v’} = \pmb{v_{\perp}‘} + \pmb{v_{\parallel}’}$。

我们可以将这些向量定义为纯四元数：

$$
\begin{aligned}
v &= [0, \pmb{v}]\
v_{\perp} &= [0, \pmb{v_{\perp}}]\
v_{\parallel} &= [0, \pmb{v_{\parallel}}]\
v’ &= [0, \pmb{v’}]\
v_{\perp}’ &= [0, \pmb{v_{\perp}‘}]\
v_{\parallel}’ &= [0, \pmb{v_{\parallel}'}]\
u &= [0, \pmb{u}]
\end{aligned}
$$

那么我们就能得到

$$
v = v_{\parallel} + v_{\perp} \qquad v’ = v_{\parallel}’ + v_{\perp}’
$$

和之前一样，我们这里也分开讨论 $v_{\perp}$ 和 $v_{\parallel}$ 的情况。

$v_{\perp}$ 的旋转

我们在上一篇推导过，如果一个向量 $\pmb{v_{\perp}}$ 正交于旋转轴 $\pmb{u}$，那么

$$
\pmb{v_{\perp}'} = \cos(\theta)\pmb{v_{\perp}} + \sin(\theta)(\pmb{u}\times\pmb{v_{\perp}})
$$

而且，对于两个纯四元数 $q_{1} = [0, \pmb{v}]$，$q_{2} = [0, \pmb{u}]$，那么它们的乘积为 $q_{1}q_{2} = [-\pmb{v}\cdot\pmb{u}, \pmb{v}\times\pmb{u}]$，类似地，
$$
uv_{\perp} = [-\pmb{u}\cdot\pmb{v_{\perp}}, \pmb{u}\times\pmb{v_{\perp}}]
$$
因为 $\pmb{v_{\perp}}$ 正交于 $\pmb{u}$，所以 $\pmb{u}\cdot\pmb{v_{\perp}} = 0$，也就是说，
$$
\begin{aligned}
uv_{\perp} &= [0, \pmb{u}\times\pmb{v_{\perp}}]\
&= \pmb{u}\times\pmb{v_{\perp}}
\end{aligned}
$$
将这个等式以及之前定义的纯四元数代入，而且四元数乘法遵守分配律，我们可以获得：
$$
\begin{aligned}
v_{\perp}’ &= \cos(\theta)v_{\perp} + \sin(\theta)(uv_{\perp})\
&= (\cos(\theta) + \sin(\theta)u)v_{\perp}
\end{aligned}
$$

可以注意到，如果我们将 $(\cos(\theta) + \sin(\theta)u)$ 看作是一个四元数，我们就能将旋转写成四元数的乘积了。到此为止，我们已经将旋转与四元数的积联系起来了。如果令 $q = \cos(\theta) + \sin(\theta)u$，我们能得到
$$
v_{\perp}’ = qv_{\perp}
$$

我们可以对 $q$ 继续进行变形：
$$
\begin{aligned}
q &= \cos(\theta) + \sin(\theta)u\
&= [\cos(\theta), \pmb{0}] + [0, \sin(\theta)\pmb{u}]\
&= [\cos(\theta), \sin(\theta)\pmb{u}]\
\end{aligned}
$$

也就是说，如果旋转轴 $\pmb{u}$ 的坐标为 $\begin{bmatrix}u_{x}\ u_{y}\ u_{z}\end{bmatrix}$，旋转角为 $\theta$，那么完成这一旋转所需的四元数 $q$ 可以构造为
$$
q = \cos(\theta) + \sin(\theta)u_{x}i + \sin(\theta)u_{y}j + \sin(\theta)u_{z}k
$$
这样我们就完成了对 $v_{\perp}$ 的旋转，我们可以得到下面这个定理：

Theorem 8：3D 旋转公式（四元数型，正交情况）
当 $\pmb{v_{\perp}}$ 正交于旋转轴 $\pmb{u}$ 时，旋转 $\theta$ 角度之后的 $\pmb{v_{\perp}‘}$ 可以使用四元数乘法来获得，令 $v_{\perp} = [0, \pmb{v_{\perp}}]$，$q = [\cos(\theta), \sin(\theta)\pmb{u}]$，那么：
$$
v_{\perp}’ = qv_{\perp}
$$

这个四元数 $q$ 的模长为 1，它是一个单位四元数，它所代表的变换不会对原向量进行缩放，是一个纯旋转。
$$
\begin{aligned}
\lVert q \rVert &= \sqrt{\cos^2(\theta) + (\sin(\theta)\pmb{u}\cdot\sin(\theta)\pmb{u})}\
&= \sqrt{\cos^2(\theta) + \sin^2(\theta)(\pmb{u}\cdot\pmb{u})}\
&= \sqrt{\cos^2(\theta) + \sin^2(\theta)(\lVert\pmb{u}\rVert^2)}\
&= \sqrt{\cos^2(\theta) + \sin^2(\theta)}\
&= 1
\end{aligned}
$$

$v_{\parallel}$ 的旋转

接下来是平行于旋转轴的 $v_{\parallel}$，由于它平行于旋转轴，所以旋转不会对它作出任何的变换，也就是说：

Theorem 9：3D 旋转公式（四元数型，平行情况）
当 $\pmb{v_{\parallel}}$ 平行于旋转轴 $\pmb{u}$ 时，旋转 $\theta$ 角度之后的 $\pmb{v_{\parallel}‘}$ 可以用四元数写为：
$$
v_{\parallel}’ = v_{\parallel}
$$

$v$ 的旋转

$$
\begin{aligned}
v’ &= v_{\parallel}’ + v_{\perp}'\
&= v_{\parallel} + qv_{\perp} \qquad (其中 q = [\cos(\theta), \sin(\theta)\pmb{u}])
\end{aligned}
$$

在进一步化简前，我们需要证明几个引理：

Lemma 1
如果 $q = [\cos(\theta), \sin(\theta)\pmb{u}]$，而且 $\pmb{u}$ 为单位向量，那么 $q^2 = qq = [\cos(2\theta), \sin(2\theta)\pmb{u}]$

$Proof$.

$$
\begin{aligned}
q^2 &= [\cos(\theta), \sin(\theta)\pmb{u}] \cdot [\cos(\theta), \sin(\theta)\pmb{u}]\
&= [\cos^2(\theta) - (\sin(\theta)\pmb{u}\cdot\sin(\theta)\pmb{u}), (\cos(\theta)\sin(\theta) + \sin(\theta)\cos(\theta))\pmb{u} + (\sin(\theta)\pmb{u}\times\sin(\theta)\pmb{u})]\
&= [\cos^2(\theta) - \sin^2(\theta)\lVert\pmb{u}\rVert^2, 2\sin(\theta)\cos(\theta)\pmb{u} + \pmb{0}]\
&= [\cos^2(\theta) - \sin^2(\theta), 2\sin(\theta)\cos(\theta)\pmb{u}]\
&= [\cos(2\theta), \sin(2\theta)\pmb{u}]
\end{aligned}
$$

这个引理的几何意义是，如果沿着同一个轴 $\pmb{u}$ 连续旋转 $\theta$ 度两次，那么所作出的变换等同于直接沿着 $\pmb{u}$ 旋转 $2\theta$ 度

那么，我们就能够对原本的旋转公式进行变形了

$$
\begin{aligned}
v’ &= v_{\parallel} + qv_{\perp} \qquad\qquad (q = [\cos(\theta), \sin(\theta)\pmb{u}])\
&= 1 \cdot v_{\parallel} + qv_{\perp}\
&= pp^{-1}v_{\parallel} + ppv_{\perp} \quad (令 q = p^2，则 p = [\cos(\frac{1}{2}\theta), \sin(\frac{1}{2}\theta)\pmb{u}])
\end{aligned}
$$

在这里，我们引入了一个新的四元数 $p = [\cos(\frac{1}{2}\theta), \sin(\frac{1}{2}\theta)\pmb{u}]$。根据刚刚证明的引理，我们可以验证
$$
\begin{aligned}
pp &= p^2\
&= [\cos(2\cdot\frac{1}{2}\theta), \sin(2\cdot\frac{1}{2}\theta)\pmb{u}]\
&= [\cos(\theta), \sin(\theta)\pmb{u}] = q
\end{aligned}
$$

和 $q$ 一样，$\lVert p \rVert = 1$，$p$ 也是一个单位四元数，也就是说
$$
p^{-1} = p^*
$$

将这个结果代入之前的等式中
$$
\begin{aligned}
v’ &= pp^{-1}v_{\parallel} + ppv_{\perp}\
&= pp^*v_{\parallel} + ppv_{\perp}
\end{aligned}
$$

我们还需再证明两个引理：

Lemma 2
假设 $v_{\parallel} = [0, \pmb{v_{\parallel}}]$ 是一个纯四元数，而 $q = [\alpha, \beta\pmb{u}]$，其中 $\pmb{u}$ 是一个单位向量，$\alpha，\beta \in \mathbb{R}$，在这种条件下，如果 $\pmb{v_{\parallel}}$ 平行于 $\pmb{u}$，那么 $qv_{\parallel} = v_{\parallel}q$

$Proof$.

$$
\begin{aligned}
LHS &= qv_{\parallel}\
&= [\alpha, \beta\pmb{u}]\cdot[0, \pmb{v_{\parallel}}]\
&= [0 - \beta\pmb{u}\cdot\pmb{v_{\parallel}}, \alpha\pmb{v_{\parallel}} + \pmb{0} + \beta\pmb{u}\times\pmb{v_{\parallel}}]\
&= [-\beta\pmb{u}\cdot\pmb{v_{\parallel}}, \alpha\pmb{v_{\parallel}}] \qquad (\pmb{v_{\parallel}} 平行于 \pmb{u}，所以 \beta\pmb{u}\times\pmb{v_{\parallel}} = \pmb{0})
\end{aligned}
$$
$$
\begin{aligned}
RHS &= v_{\parallel}q\
&= [0, \pmb{v_{\parallel}}]\cdot[\alpha, \beta\pmb{u}]\
&= [0 - \pmb{v_{\parallel}}\cdot\beta\pmb{u}, \pmb{0} + \alpha\pmb{v_{\parallel}} + \pmb{v_{\parallel}}\times\beta\pmb{u}]\
&= [-\pmb{v_{\parallel}}\cdot\beta\pmb{u}, \alpha\pmb{v_{\parallel}}] \qquad ({v_{\parallel}} 平行于 \pmb{u}，所以 \pmb{v_{\parallel}}\times\beta\pmb{u} = \pmb{0})\
&= [-\beta\pmb{u}\cdot\pmb{v_{\parallel}}, \alpha\pmb{v_{\parallel}}] = LHS \qquad (点乘遵守交换律)
\end{aligned}
$$

Lemma 3
假设 $v_{\perp} = [0, \pmb{v_{\perp}}]$ 是一个纯四元数，而 $q = [\alpha, \beta\pmb{u}]$，其中 $\pmb{u}$ 是一个单位向量，$\alpha，\beta \in \mathbb{R}$，在这种条件下，如果 $\pmb{v_{\perp}}$ 正交于 $\pmb{u}$，那么 $qv_{\perp} = v_{\perp}q^*$

$Proof$.

$$
\begin{aligned}
LHS &= qv_{\perp}\
&= [\alpha, \beta\pmb{u}]\cdot[0, \pmb{v_{\perp}}]\
&= [0 - \beta\pmb{u}\cdot\pmb{v_{\perp}}, \alpha\pmb{v_{\perp}} + \pmb{0} + \beta\pmb{u}\times\pmb{v_{\perp}}]\
&= [0, \alpha\pmb{v_{\perp}} + \beta\pmb{u}\times\pmb{v_{\perp}}] \qquad (\pmb{v_{\perp}} 正交于 \pmb{u}，所以 \beta\pmb{u}\cdot\pmb{v_{\perp}} = 0)
\end{aligned}
$$
$$
\begin{aligned}
RHS &= v_{\perp}q^*\
&= [0, \pmb{v_{\perp}}]\cdot[\alpha, -\beta\pmb{u}]\
&= [0 + \pmb{v_{\perp}}\cdot\beta\pmb{u}, \pmb{0} + \alpha\pmb{v_{\perp}} + \pmb{v_{\perp}}\times(-\beta\pmb{u})]\
&= [0, \alpha\pmb{v_{\perp}} + \pmb{v_{\perp}}\times(-\beta\pmb{u})] \qquad ({v_{\perp}} 正交于 \pmb{u}，所以 \pmb{v_{\perp}}\cdot\beta\pmb{u} = 0)\
&= [0, \alpha\pmb{v_{\perp}} - (-\beta\pmb{u})\times\pmb{v_{\perp}}] \qquad (\pmb{a}\times\pmb{b} = -\pmb{b}\times\pmb{a})\
&= [0, \alpha\pmb{v_{\perp}} + \beta\pmb{u}\times\pmb{v_{\perp}}] = LHS
\end{aligned}
$$

现在，我们能对之前的公式做出最后的变形了：
$$
\begin{aligned}
v’ &= pp^v_{\parallel} + ppv_{\perp}\
&= pv_{\parallel}p^ + pv_{\perp}p^\
&= p(v_{\parallel} + v_{\perp})p^\
&= pvp^*
\end{aligned}
$$

我们可以将上述推导总结为一个定理：

Theorem 10：3D 旋转公式（四元数型，一般情况）
任意向量 $\pmb{v}$ 沿着以单位向量定义的旋转轴 $\pmb{u}$ 旋转 $\theta$ 度之后的 $\pmb{v’}$ 可以使用四元数乘法来获得。令 $v = [0, \pmb{v}]$，$q = [\cos(\frac{1}{2}\theta), \sin(\frac{1}{2}\theta)\pmb{u}]$，那么：
$$
v’ = qvq^* = qvq^{-1}
$$

如果我们有 $q = [\cos(\theta), \sin(\theta)\pmb{u}]$，那么 $v’ = qvq^*$ 可以将 $\pmb{v}$ 沿着 $\pmb{u}$ 旋转 $2\theta$ 度。

虽然这个公式非常简洁，但是不够直观，想了解它的真正含义的话，还需将它还原到变形之前的式子：
$$
v’ = qvq^* = qq^*v_{\parallel} + qqv_{\perp} = v_{\parallel} + q^2v_{\perp}
$$

也就是说，$qvq^$ 这个变换，对 $v$ 平行于旋转轴的分量 $v_{\parallel}$ 实施的变换是 $qq^$，这两个变换完全抵消了，也就是没有旋转，而对于正交于旋转轴的分量 $v_{\perp}$ 则实施的是两次变换 $q^2 = qq$，将它旋转 $\frac{\theta}{2} + \frac{\theta}{2} = \theta$ 度。

实际上，这个公式和上一篇推导的向量型旋转公式完全等价，证明可能会用到 $\pmb{a}\times(\pmb{b}\times\pmb{c}) = (\pmb{a}\cdot\pmb{c})\pmb{b} - (\pmb{a}\cdot\pmb{b})\pmb{c}$ 这个公式
$$
qvq^* = [0, \cos(\theta)\pmb{v} + (1 - \cos(\theta))(\pmb{u}\cdot\pmb{v})\pmb{u} + \sin(\theta)(\pmb{u}\times\pmb{v})]
$$

因为所有的旋转四元数的实部都只是一个角度的余弦值，假设有一个单位四元数 $q = [a, \pmb{b}]$，那么我们可以直接得到
$$
\frac{\theta}{2} = \arccos(a) \qquad \pmb{u} = \frac{\pmb{b}}{\sin(\arccos(a))}
$$

3D旋转的矩阵形式

左乘一个四元数 $q = a + bi + cj + dk$ 等同于下面这个矩阵
$$
L(q) = \begin{bmatrix}
a&-b&-c&-d\
b&a&-d&c\
c&d&a&-b\
d&-c&b&a\
\end{bmatrix}
$$
而右乘 $q$ 等同于这个矩阵
$$
R(q) = \begin{bmatrix}
a&-b&-c&-d\
b&a&d&-c\
c&-d&a&b\
d&c&-b&a\
\end{bmatrix}
$$

所以，我们可以利用这两个公式将 $v’ = qvq^$ 写成矩阵形式。假设 $a = \cos(\frac{\theta}{2})，b = \sin(\frac{\theta}{2})u_{x}，c = \sin(\frac{\theta}{2})u_{y}，d = \sin(\frac{\theta}{2})u_{z}，q = a + bi + cj + dk$，我们就能得到：
$$
\begin{aligned}
qvq^ &= L(q)R(q^)v \qquad (或者 R(q^)L(q)v，它们是等价的)\
&= \begin{bmatrix}
a&-b&-c&-d\
b&a&-d&c\
c&d&a&-b\
d&-c&b&a\
\end{bmatrix}
\begin{bmatrix}
a&b&c&d\
-b&a&-d&c\
-c&d&a&-b\
-d&-c&b&a\
\end{bmatrix}v \qquad (注意 R(q^) = R(q)^T)\
&= \begin{bmatrix}
a^2 + b^2 + c^2 + d^2&ab - ab - cd + cd&ac + bd - ac - bd&ad - bc + bc - ad\
ab - ab + cd - cd&b^2 + a^2 - d^2 - c^2&bc - ad - ad + bc&bd + ac + bd + ac\
ac - bd - ac + bd&bc + ad + ad + bc&c^2 - d^2 + a^2 - b^2&cd + cd - ab - ab\
ad + bc - bc - ad&bd - ac + bd - ac&cd + cd + ab + ab&d^2 - c^2 - b^2 + a^2\
\end{bmatrix}v
\end{aligned}
$$
因为 $a^2 + b^2 + c^2 + d^2 = 1$，这个式子能化简为
$$
qvq^ =
\begin{bmatrix}
1&0&0&0\
0&1 - 2c^2 - 2d^2&2bc - 2ad&2ac + 2bd\
0&2bc + 2ad&1 - 2b^2 - 2d^2&2cd - 2ab\
0&2bd - 2ac&2ab + 2cd&1 - 2b^2 - 2c^2\
\end{bmatrix}v
$$

这样我们就得到了 3D 旋转的矩阵形式。因为矩阵的第一行和第一列不会对 $v$ 进行任何变换，我们可以将它压缩成 3 $\times$ 3 矩阵（用作 3D 向量的变换）：

Theorem 11：3D 旋转公式（矩阵型）
任意向量 $\pmb{v}$ 沿着以单位向量定义的旋转轴 $\pmb{u}$ 旋转 $\theta$ 度之后的 $\pmb{v’}$ 可以使用矩阵乘法来获得。令 $a = \cos(\frac{\theta}{2})，b = \sin(\frac{\theta}{2})u_{x}，c = \sin(\frac{\theta}{2})u_{y}，d = \sin(\frac{\theta}{2})u_{z}$，那么：
$$
v’ =
\begin{bmatrix}
1 - 2c^2 - 2d^2&2bc - 2ad&2ac + 2bd\
2bc + 2ad&1 - 2b^2 - 2d^2&2cd - 2ab\
2bd - 2ac&2ab + 2cd&1 - 2b^2 - 2c^2\
\end{bmatrix}v
$$

虽然 3D 旋转的矩阵形式可能不如四元数形式简单，而且占用更多的空间，但是对于大批量的变换，使用预计算好的矩阵是比四元数乘法更有效率的。

旋转的复合

假设有两个表示沿着不同轴，不同角度旋转的四元数 $q_{1}$，$q_{2}$，我们先对 $v$ 进行 $q_{1}$ 的变换，再进行 $q_{2}$ 的变换。

首先，我们实施 $q_{1}$ 的变换，变换后的 $v’$ 为
$$
v’ = q_{1}vq_{1}^*
$$
接下来，对 $v’$ 进行 $q_{2}$ 的变换，得到 $v’‘$
$$
\begin{aligned}
v’’ &= q_{2}v’q_{2}^\
&= q_{2}q_{1}vq_{1}^q_{2}^
\end{aligned}
$$
我们需要对这两个变换进行复合，写为一个等价变换的形式：
$$
v’’ = q_{net}vq_{net}^
$$

为了写成上面这种形式，我们还需要一个引理：

Lemma 4
对任意四元数 $q_{1} = [s, \pmb{v}]、q_{2} = [t, \pmb{u}]$
$$
q_{1}^q_{2}^ = (q_{2}q_{1})^*
$$

$Proof$.

$$
\begin{aligned}
LHS &= q_{1}^q_{2}^\
&= [s, -\pmb{v}]\cdot[t, -\pmb{u}]\
&= [st - (-\pmb{v})\cdot(-\pmb{u}), s(-\pmb{u}) + t(-\pmb{v}) + (-\pmb{v})\times(-\pmb{u})]\
&= [st - \pmb{v}\cdot\pmb{u}, -s\pmb{u} - t\pmb{v} + \pmb{v}\times\pmb{u}]
\end{aligned}
$$
$$
\begin{aligned}
RHS &= (q_{2}q_{1})^\
&= ([t, \pmb{u}]\cdot[s, \pmb{v}])^\
&= [ts - \pmb{u}\cdot\pmb{v}, t\pmb{v} + s\pmb{u} + \pmb{u}\times\pmb{v}]\
&= [st - \pmb{v}\cdot\pmb{u}, -s\pmb{u} - t\pmb{v} + \pmb{v}\times\pmb{u}] = LHS
\end{aligned}
$$

所以我们能得到
$$
\begin{aligned}
v’’ &= q_{2}q_{1}vq_{1}^q_{2}^\
&= (q_{2}q_{1})v(q_{2}q_{1})^*\
\end{aligned}
$$

这也就是说，$q_{net} = q_{2}q_{1}$。注意四元数乘法的顺序，我们先进行的是 $q_{1}$ 的变换，再进行 $q_{2}$ 的变换。这和矩阵与函数的复合非常相似，都是从右往左叠加。

要注意的是，$q_{1}$ 与 $q_{2}$ 的等价旋转 $q_{net}$ 并不是分别沿着 $q_{1}$ 和 $q_{2}$ 的两个旋转轴进行的两次旋转。它是沿着一个全新的旋转轴进行的一次等价旋转，仅仅只有旋转的结果相同。

虽然我们讨论的是两个旋转的复合，但是它可以很容易地推广到多个旋转的复合。比如说我们还需要进行第三个旋转 $q_{3}$，那么
$$
\begin{aligned}
v’‘’ &= q_{3}(q_{2}q_{1})v(q_{2}q_{1})^q_{3}^\
&= (q_{3}q_{2}q_{1})v(q_{3}q_{2}q_{1})^*
\end{aligned}
$$
它的等价旋转就是 $q_{net} = q_{3}q_{2}q_{1}$

双倍覆盖

四元数与 3D 旋转的关系并不是一对一的，同一个 3D 旋转可以使用两个不同的四元数来表示。对任意的四元数 $q = [\cos(\frac{\theta}{2}), \sin(\frac{\theta}{2})\pmb{u}]$，$q$ 与 $-q$ 代表的是同一个旋转。如果 $q$ 表示的是沿着旋转轴 $\pmb{u}$ 旋转 $\theta$ 度，那么 $-q$ 代表的是沿着相反的旋转轴 $-\pmb{u}$ 旋转 $(2\pi - \theta)$ 度：
$$
\begin{aligned}
-q &= [-\cos(\frac{\theta}{2}), -\sin(\frac{\theta}{2})\pmb{u}]\
&= [\cos(\pi - \frac{\theta}{2}), \sin(\pi - \frac{\theta}{2})(-\pmb{u})]\qquad (\cos(\pi - \theta) = -\cos(\theta), \sin(\pi - \theta) = \sin(\theta))
\end{aligned}
$$
所以，这个四元数旋转的角度为 $2(\pi - \frac{\theta}{2}) = 2\pi - \theta$。从下面的图中我们可以看到，这两个旋转是完全等价的：

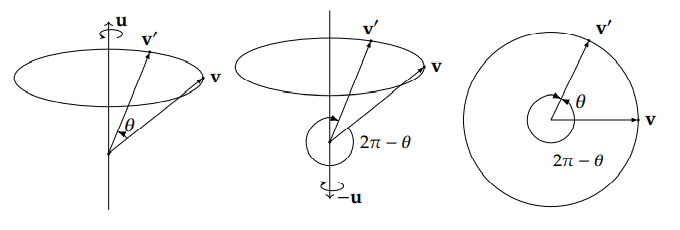
其实从四元数的旋转公式中也能推导出相同的结果
$$
(-q)v(-q)^* = (-1)^2qvq^* = qvq^*
$$

所以，我们经常说单位四元数与 3D 旋转有一个“2对1满射同态”关系，或者说单位四元数“双倍覆盖”了 3D 旋转。

因为这个映射是满射，我们可以说所有的单位四元数都对应着一个 3D 旋转。或者说，一个四维单位超球面（也叫做 $\mathbb{S}^3$）上任意一点所对应的四元数（$\lVert q \rVert = 1$）都对应着一个 3D 旋转。

有一点需要注意的是，虽然 $q$ 与 $-q$ 是两个不同的四元数，但是由于旋转矩阵中的每一项都包含了四元数两个分量的乘积，它们的旋转矩阵是完全相同的。旋转矩阵并不会出现双倍覆盖的问题。

指数形式

在讨论复数的时候，我们利用欧拉公式将 2D 的旋转写成了 $v’ = e^{i\theta}v$ 这样的指数形式。实际上，我们也可以利用四元数将 3D 旋转写成类似的形式。

类似于复数的欧拉公式，四元数也有一个类似的公式，如果 $\pmb{u}$ 是一个单位向量，那么对于单位四元数 $u = [0, \pmb{u}]$，有
$$
e^{u\theta} = \cos(\theta) + u\sin(\theta) = \cos(\theta) + \pmb{u}\sin(\theta)
$$
也就是说，$q = [\cos(\theta), \sin(\theta)\pmb{u}]$ 可以使用指数表示为 $e^{u\theta}$。这个公式的证明与欧拉公式的证明非常类似，直接使用级数展开就可以了。

$Proof$.

我们知道，$e^{x}$，$\sin(x)$，$\cos(x)$ 分别能用泰勒级数展开为：

$$
\begin{aligned}
e^{x} &= \sum_{n=0}^{\infty}{\frac{x^{n}}{n!}} = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \dots\
\sin(x) &= \sum_{n=0}^{\infty}{\frac{(-1)^n}{(2n + 1)!}x^{2n + 1}} = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \dots\
\cos(x) &= \sum_{n=0}^{\infty}{\frac{(-1)^n}{(2n)!}x^{2n}} = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \dots\
\end{aligned}
$$

我们可以将 $x = u\theta$ 代入 $e^x$，得到
$$
\begin{aligned}
LHS = e^{u\theta} &= \sum_{n=0}^{\infty}{\frac{(u\theta)^n}{n!}}\
&= 1 + u\theta + \frac{(u\theta)^2}{2!} + \frac{(u\theta)^3}{3!} + \frac{(u\theta)^4}{4!} + \frac{(u\theta)^5}{5!} + \dots\
&= 1 + u\theta + \frac{u^2\theta^2}{2!} + \frac{u^3\theta^3}{3!} + \frac{u^4\theta^4}{4!} + \frac{u^5\theta^5}{5!} + \dots\
\end{aligned}
$$

因为 $u^2 = [-\pmb{u}\cdot\pmb{u}, \pmb{0}] = -\lVert u \rVert^2 = -1$，我们可以对 $e^{u\theta}$ 进一步化简
$$
\begin{aligned}
LHS &= 1 + u\theta + \frac{u^2\theta^2}{2!} + \frac{uu^2\theta^3}{3!} + \frac{(u^2)^2\theta^4}{4!} + \frac{u(u^2)^2\theta^5}{5!} + \dots\
&= 1 + u\theta - \frac{\theta^2}{2!} - \frac{u\theta^3}{3!} + \frac{\theta^4}{4!} + \frac{u\theta^5}{5!} - \dots\
\end{aligned}
$$

同理，将 $\theta$ 代入 $\cos(x)$ 和 $\sin(x)$，
$$
\begin{aligned}
\sin(\theta) &= \sum_{n=0}^{\infty}{\frac{(-1)^n}{(2n + 1)!}\theta^{2n + 1}}\
&= \theta - \frac{\theta^3}{3!} + \frac{\theta^5}{5!} - \frac{\theta^7}{7!} + \dots\
\
\cos(\theta) &= \sum_{n=0}^{\infty}{\frac{(-1)^n}{(2n)!}\theta^{2n}}\
&= 1 - \frac{\theta^2}{2!} + \frac{\theta^4}{4!} - \frac{\theta^6}{6!} + \dots\
\end{aligned}
$$

所以，
$$
\begin{aligned}
RHS &= \cos(\theta) + u\sin(\theta)\
&= \sum_{n=0}^{\infty}{\frac{(-1)^n}{(2n)!}\theta^{2n}} + u\sum_{n=0}^{\infty}{\frac{(-1)^n}{(2n + 1)!}\theta^{2n + 1}}\
&= 1 + u\theta - \frac{\theta^2}{2!} - \frac{u\theta^3}{3!} + \frac{\theta^4}{4!} + \frac{u\theta^5}{5!} - \dots = LHS
\end{aligned}
$$

因为 $\pmb{u}$ 是一个单位向量，$u^2 = [-\pmb{u}\cdot\pmb{u}, \pmb{0}] = -\lVert u \rVert^2 = -1$，这与欧拉公式中的 $i$ 是非常类似的。

有了指数型的表示方式，我们就能够将之前四元数的旋转公式改写为指数形式了：

Theorem 12：3D 旋转公式（指数型）
任意向量 $\pmb{v}$ 沿着以单位向量定义的旋转轴 $\pmb{u}$ 旋转 $\theta$ 度之后的 $\pmb{v’}$ 可以使用四元数的指数表示。令 $v = [0, \pmb{v}]，u = [0, \pmb{u}]$，那么：
$$
v’ = e^{u\frac{\theta}{2}}ve^{-u\frac{\theta}{2}}
$$

有了四元数的指数定义，我们就能够定义四元数的更多运算了，首先是自然对数 $\log$，对任意单位四元数 $q = [\cos(\theta), \sin(\theta)\pmb{u}]$，
$$
\log(q) = \log(e^{u\theta}) = [0, \pmb{u}\theta]
$$
接下来是四元数的幂运算
$$
q^t = (e^{u\theta})^t = e^{u(t\theta)} = [\cos(t\theta), \sin(t\theta)\pmb{u}]
$$
可以看到，一个单位四元数的 $t$ 次幂等同于将它的旋转角缩放至 $t$ 倍，并且不会改变它的旋转轴（$u$ 必须是单位向量，所以一般不能与 $t$ 结合）。这些运算会在之后讨论四元数插值时非常有用。