四元数和三维旋转(三)

四元数插值

假设有两个旋转变换 $q_0 = [\cos(\theta_{0}), \sin(\theta_{0})\pmb{u_0}]$ 和 $q_1 = [\cos(\theta_{1}), \sin(\theta_{1})\pmb{u_1}]$，我们希望找出一些中间变换 $q_{t}$，让初始变换 $q_{0}$ 能够平滑地过渡到最终变换 $q_{1}$，$t$ 的取值可以是 $t \in [0, 1]$，当 $t = 0$ 时 $q_{t}$ 等同于初始变换 $q_{0}$，而 $t = 1$ 时 $q_{t}$ 等同于最终变换 $q_{1}$。

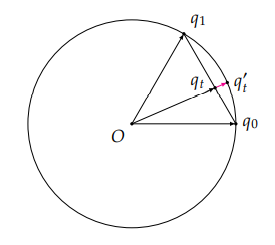
由于插值的对象是两个变换，想象起来可能非常困难，我们不妨假设 3D 空间中有任意一个向量 $v$，那么 $q_{0}$ 会将 $v$ 变换到 $v_{0} = q_{0}vq_{0}^$，而 $q_{1}$ 会将 $v$ 变换到 $v_{1} = q_{1}vq_{1}^$。我们需要找出中间向量 $v_{t} = q_{t}vq_{t}^*$ 所对应的变换 $q_{t}$，使 $v$ 旋转到 $v_{0}$ 与 $v_{1}$ 中间的某个位置 $v_{t}$:

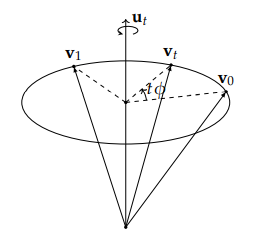
我们可以看到，这个旋转的变化量其实对应的仍是一个旋转。它将由 $q_{0}$ 变换到 $v_{0}$ 的向量进一步旋转到 $v_{t}$。这个旋转拥有某一个固定的旋转轴 $\pmb{u_{t}}$，我们只需要缩放这个变换所对应的角度 $\phi$ 就能够达到插值的目的了。

那么，现在的问题是，我们该怎么获得这个旋转的变化量。我们不妨考虑一下什么变换 $\Delta q$ 能将已经旋转到 $v_{0}$ 的向量 $v$ 直接变换到 $v_{1}$。这其实就是一个旋转的复合，我们先进行 $q_{0}$ 变换，再进行 $\Delta q$ 变换，它们复合的结果需要等于 $q_{1}$ 变换，也就是说：
$$
\Delta qq_{0} = q_{1}
$$
那么，
$$
\begin{aligned}
\Delta qq_{0}q_{0}^{-1} &= q_{1}q_{0}^{-1}\
\
\Delta q &= q_{1}q_{0}^{-1}\
\end{aligned}
$$

因为所有的旋转 $q$ 都是单位四元数，$q^{-1} = q^$，它又可以写成：
$$
\Delta q = q_{1}q_{0}^
$$

如果我们对 $\Delta q$ 取 $t$ 次方，$(\Delta q)^t$ 就能缩放这个旋转所对应的角度了。所以，我们就能得出插值的公式：

$$
q_t = Slerp(q_0, q_1; t) = (q_1q_0^)^tq_0
$$
可以发现，当 $t = 0$ 时，$q_t = q_0$；而当 $t = 1$ 时，$q_t = q_1$；如果 $t$ 为中间值，比如说 $t = 0.4$ 时，$q_t = (q_{1}q_{0}^)^{0.4}q_{0}$，它会先进行 $q_0$ 变换将 $v$ 变换到 $v_0$，并在此基础上向 $v_1$ 旋转 40%.

这个插值方法称为Slerp，但它涉及到多个四元数的乘法，而且还包含幂运算，实际应用中效率很低。为了理解它我们还需要研究一下 3D 空间的旋转与四元数的 4D 向量空间之间的关系

3D空间旋转变化量 vs. 四元数4D向量空间夹角

为了探讨这个关系，我们来实际计算一下 $\Delta q$。由于这个关系和角度有关，我们只需要关心 $\Delta q$ 的实部就可以了：

$$
\begin{aligned}
\Delta q &= q_{1}q_{0}^*\
&= [\cos(\theta_{1}), \sin(\theta_{1})\pmb{u_1}][\cos(\theta_{0}), -\sin(\theta_{0})\pmb{u_0}]\
&= [\cos(\theta_{0})\cos(\theta_{1}) - (\sin(\theta_{1})\pmb{u_1})\cdot(-\sin(\theta_{0})\pmb{u_0}), \dots]\
&= [\cos(\theta_{0})\cos(\theta_{1}) + (\sin(\theta_{1})\pmb{u_1})\cdot(\sin(\theta_{0})\pmb{u_0}), \dots]\
\end{aligned}
$$

如果将 $q_{0}$ 和 $q_{1}$ 看作是两个四维向量，我们可以发现 $\Delta q$ 的实部正好就是 $q_{0}$ 和 $q_{1}$ 点乘的结果 $q_{0} \cdot q_{1}$，因为 $q_{0}$ 和 $q_{1}$ 都是单位四元数，$q_{0} \cdot q_{1}$ 正好是这两个四元数在 4D 空间中夹角的余弦值，我们将这个夹角称为 $\theta$，那么 $q_{0} \cdot q_{1} = \cos(\theta)$

我们又知道，$\Delta q$ 表示的也是一个旋转，而如果它代表的旋转的角度是 $2\phi$，那么 $\Delta q$ 的实数部为 $\Delta q = [\cos(\phi), \dots]$。所以
$$
\Delta q = [\cos(\phi), \dots] = [\cos(\theta), \dots]\
\cos(\phi) = \cos(\theta)
$$

因为 $\phi$ 和 $\theta$ 都是夹角，$\phi，\theta \in [0, \pi]$，所以这个方程有唯一的解
$$
\phi = \theta
$$

这也就是说，$q_{0}$ 与 $q_{1}$ 作为向量在 4D 四元数空间中的夹角 $\theta$，正好是它们旋转变化量 $\Delta q$ 的所代表旋转的角度的一半，即 $\theta = \frac{1}{2}(2\phi)$。所以，我们可以直接用插值向量的方法对旋转进行插值。

为了更直观的理解这层关系，请看下面这两幅图。虽然四元数是出于四维空间之内的，但是因为只有两个四元数，我们可以将它们投影到一个二维的圆上来，也就是左图。右侧则是 3D 空间中发生的旋转改变

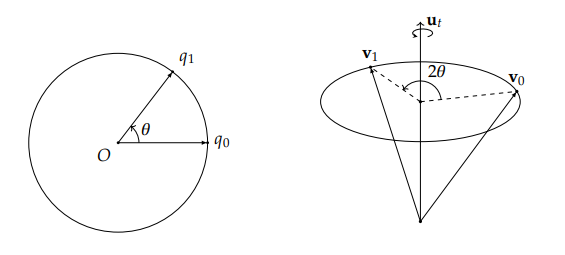
可以看到，当 $q_{1}$ 与 $q_{0}$ 之间的夹角为 $\theta$ 时，旋转的变化量正好是 $2\theta$。如果我们在圆上有一个单位四元数 $q_{t}$，使得它与 $q_{0}$ 的夹角为 $t\theta$，与 $q_{1}$ 的夹角为 $(1 - t)\theta$，那么我们就能保证在 3D 空间中，它相对于 $q_{0}$ 的旋转变化量为 $2t\theta$，相对于 $q_{1}$ 的旋转变化量为 $2(1 - t)\theta$。

现在，两个单位四元数的插值就被我们简化为了一个圆上（其实是超球面的一部分）两个向量的插值，我们能直接套用向量的插值公式对两个四元数进行插值。接下来，我们就来讨论如何对两个向量进行插值。

Lerp, Nlerp, Slerp

不论是哪种插值方法，我们都希望将中间向量 $v_{t}$ 写为初始向量 $v_{0}$ 和最终向量 $v_{1}$ 的线性组合，也就是说：
$$
v_{t} = \alpha v_{0} + \beta v_{1}
$$
其中，系数 $\alpha$ 与 $\beta$ 都是 $t$ 的函数。不同的插值方法只是拥有不同的系数而已。

Lerp

首先是两个向量插值最简单的一种形式：线性插值，也叫做“Lerp”。Lerp 会沿着一条直线进行插值，如果将 $\pmb{v_{0}}$ 和 $\pmb{v_{1}}$ 看做是三角形的两个边，那么 $\pmb{v_{t}}$ 会指向三角形的第三条边。

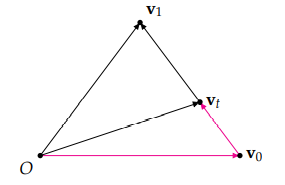
我们能将 $\pmb{v_{t}}$ 写为两个向量的和。
$$
\begin{aligned}
\pmb{v_{t}} = Lerp(\pmb{v_{0}}, \pmb{v_{1}}, t) &= \pmb{v_{0}} + t(\pmb{v_{1}} - \pmb{v_{0}})\
&= (1 - t)\pmb{v_{0}} + t\pmb{v_{1}}
\end{aligned}
$$

如果将 Lerp 的结果应用到单位四元数上，我们可以得到：
$$
q_{t} = Lerp(q_{0}, q_{1}, t) = (1 - t)q_{0} + tq_{1}
$$
当然，因为我们是沿着一条直线（也就是圆上的一个弦）进行插值的，这样插值出来的四元数并不是单位四元数。

Nlerp

虽然这样插值出来的 $q_{t}$ 并不是单位四元数，但只要将 $q_{t}$ 除以他的模长 $\lVert q_{t} \rVert$ 就能够将其转化为一个单位四元数了。

我们将这种先对向量进行插值，再进行正规化的插值方法称为正规化线性插值，或者“Nlerp”。与 Lerp 不同，Nlerp 的两个输入向量必须是单位向量，否则插值出来的结果不会经过初始和最终向量。下面分别是向量和四元数的 Nlerp 公式。

$$
v_{t} = Nlerp(\pmb{v_{0}}, \pmb{v_{1}}, t) = \frac{(1 - t)\pmb{v_{0}} + t\pmb{v_{1}}}{\lVert (1 - t)\pmb{v_{0}} + t\pmb{v_{1}} \rVert}\
\
q_{t} = Nlerp(q_{0}, q_{1}, t) = \frac{(1 - t)q_{0} + tq_{1}}{\lVert (1 - t)q_{0} + tq_{1} \rVert}
$$

Nlerp 插值仍然存在有一定的问题，当需要插值的弧比较大时，$\pmb{v_{t}}$ 的角速度会有显著的变化．我们可以来看一个例子：

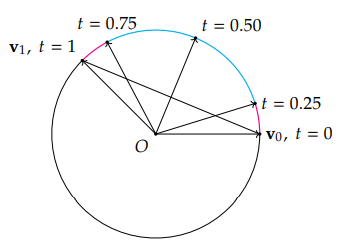
这五个 $t$ 值将整个弧和弦分割成了四个部分．虽然弦上的四段是等长的，但是四个弧是完全不相等的。$t = 0$ 到 $t = 0.25$ 之间的弧（红色）明显比 $t = 0.25$ 到 $t = 0.50$ 的弧（蓝色）要短了不少．

这也就是说，在同等时间内，$\pmb{v_{t}}$ 扫过的角度是不同的。$\pmb{v_{t}}$ 扫过的速度（或者说角速度）首先会不断地增加，到 $t = 0.50$ 之后会开始减速，所以 Nlerp 插值不能保证均匀的角速度．

Slerp

为了解决这个问题，我们可以转而对角度进行线性插值。也就是说，如果 $\pmb{v_{1}}$ 和 $\pmb{v_{2}}$ 之间的夹角为 $\theta$，那么
$$
\theta_{t} = (1 - t)\cdot 0 + t\theta = t\theta
$$
因为对角度线性插值直接是让向量在球面上的一个弧上旋转，所以又称球面线性插值，或者“Slerp”。

上面的公式并没有涉及到任何的向量，我们希望将 $\pmb{v_{t}}$ 写为 $\pmb{v_{0}}$ 和 $\pmb{v_{1}}$ 的线性组合
$$
\pmb{v_{t}} = \alpha\pmb{v_{0}} + \beta\pmb{v_{1}}
\tag{1}
$$
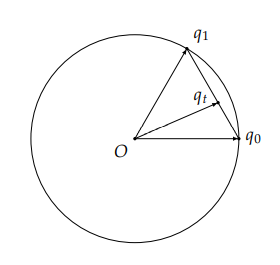
这里的 $\pmb{v_{0}}$ 和 $\pmb{v_{1}}$ 仍是单位向量，为了求出这其中的 $\alpha$ 和 $\beta$，我们需要借助图像来找出一些关系：

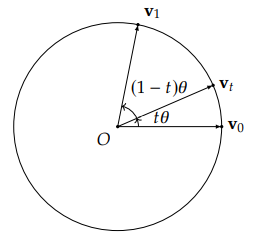
我们可以先对(1)式的两边同时点乘 $\pmb{v_{0}}$
$$
\begin{aligned}
\pmb{v_{0}}\cdot\pmb{v_{t}} &= \pmb{v_{0}}\cdot(\alpha\pmb{v_{0}} + \beta\pmb{v_{1}})\
\pmb{v_{0}}\cdot\pmb{v_{t}} &= \alpha(\pmb{v_{0}}\cdot\pmb{v_{0}}) + \beta(\pmb{v_{0}}\cdot\pmb{v_{1}})
\end{aligned}
$$
我们知道，$\pmb{v_{0}}$ 和 $\pmb{v_{t}}$ 之间的夹角是 $t\theta$，$\pmb{v_{0}}$ 与它自身之间的夹角为 0，$\pmb{v_{0}}$ 和 $\pmb{v_{1}}$ 之间的夹角是 $\theta$，而且所有的向量都是单位向量，所以
$$
\cos(t\theta) = \alpha + \beta\cos(\theta)
\tag{2}
$$
同理，我们将(1)式的两边同时点乘 $\pmb{v_{1}}$，构造第二个方程
$$
\begin{aligned}
\pmb{v_{1}}\cdot\pmb{v_{t}} &= \pmb{v_{1}}\cdot(\alpha\pmb{v_{0}} + \beta\pmb{v_{1}})\
\pmb{v_{1}}\cdot\pmb{v_{t}} &= \alpha(\pmb{v_{1}}\cdot\pmb{v_{0}}) + \beta(\pmb{v_{1}}\cdot\pmb{v_{1}})
\end{aligned}
$$

$$
\cos((1 - t)\theta) = \alpha\cos(\theta) + \beta
\tag{3}
$$

现在我们可以用(2)式和(3)式求出 $\alpha$ 和 $\beta$ 了。

由(2)式可以得到
$$
\alpha = \cos(t\theta) - \beta\cos(\theta)
\tag{4}
$$

将(4)式代入(3)式
$$
\begin{aligned}
\cos((1 - t)\theta) &= (\cos(t\theta) - \beta\cos(\theta))\cos(\theta) + \beta\
\cos((1 - t)\theta) &= \cos(t\theta)\cos(\theta) - \beta\cos^2(\theta) + \beta\
\beta(1 - \cos^2(\theta)) &= \cos((1 - t)\theta) - \cos(t\theta)\cos(\theta)\
\beta &= \frac{\cos(\theta - t\theta) - \cos(t\theta)\cos(\theta)}{\sin^2(\theta)}\
\beta &= \frac{\cos(\theta)\cos(t\theta) + \sin(\theta)\sin(t\theta) - \cos(t\theta)\cos(\theta)}{\sin^2(\theta)}\
\beta &= \frac{\sin(\theta)\sin(t\theta)}{\sin^2(\theta)}\
\beta &= \frac{\sin(t\theta)}{\sin(\theta)}
\end{aligned}
$$

将 $\beta$ 代入(4)式解出 $\alpha$
$$
\begin{aligned}
\alpha &= \cos(t\theta) - (\frac{\sin(t\theta)}{\sin(\theta)})\cos(\theta)\
&= \frac{\cos(t\theta)\sin(\theta) - \sin(t\theta)\cos(\theta)}{\sin(\theta)}\
&= \frac{\sin((1 - t)\theta)}{\sin(\theta)}
\end{aligned}
$$

将 $\alpha$ 和 $\beta$ 代回(1)式，我们可以得到向量的Slerp公式
$$
\pmb{v_{t}} = Slerp(\pmb{v_{0}}, \pmb{v_{1}}, t) = \frac{\sin((1 - t)\theta)}{\sin(\theta)}\pmb{v_{0}} + \frac{\sin(t\theta)}{\sin(\theta)}\pmb{v_{1}}
$$
类似地，我们有四元数的 Slerp 公式：
$$
q_{t} = Slerp(q_{0}, q_{1}, t) = \frac{\sin((1 - t)\theta)}{\sin(\theta)}q_{0} + \frac{\sin(t\theta)}{\sin(\theta)}q_{1}
$$
其中 $q_{0}$ 与 $q_{1}$ 之间的夹角 $\theta$ 可以直接使用它们点乘的结果来得出，即
$$
\theta = \arccos(q_{0} \cdot q_{1})
$$

这里导出的公式会比之前利用幂运算的公式要高效很多，但是它仍然涉及到三个三角函数以及一个反三角函数的运算，所以还是会比 Nlerp 要慢一点。如果要插值的角度比较小的话，Nlerp 其实相对于 Slerp 的误差并没有那么大。为了提高效率，我们经常会使用 Nlerp 来代替 Slerp。我们也能用一些数值分析的方法来近似并优化四元数的 Slerp。

除了效率问题之外，我们在实现 Slerp 时要注意，如果单位四元数之间的夹角 $\theta$ 非常小，那么 $\sin(\theta)$ 可能会由于浮点数的误差被近似为 0.0，从而导致除以 0 的错误．所以，我们在实施 Slerp 之前，需要检查两个四元数的夹角是否过小（或者完全相同）。一旦发现这种问题，我们就必须改用 Nlerp 对两个四元数进行插值，这时候 Nlerp 的误差非常小所以基本不会与真正的 Slerp 有什么区别。

双倍覆盖带来的问题

如果你还记得，两个不同的单位四元数 $q$ 与 $-q$ 对应的其实是同一个旋转，这个特性显然会对我们的插值造成一些影响．虽然 $q$ 与 $-q$ 对向量变换的最终效果是完全相同的，但是它们作为向量相差了 $\pi$ 弧度：

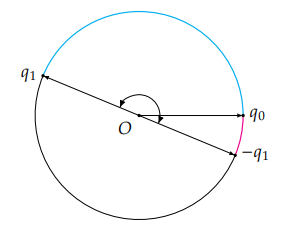
可以看到，虽然我们能够将 $q_{0}$ 向左插值至 $q_{1}$（蓝色的弧），但这会将 3D 空间中的向量旋转接近 360 度，而实际上这两个旋转相差并没有那么多，它并不是 3D 空间中的弧面最短路径。而如果我们将 $q_{0}$ 向右插值至等价的 $-q_{1}$（红色的弧），它的旋转变化量就会比插值到 $q_{1}$ 要小很多，所以 $q_{0}$ 插值到 $-q_{1}$ 才是插值的最短路径。

这也就告诉我们，在对两个单位四元数进行插值之前，我们需要先检测 $q_{0}$ 与 $q_{1}$ 之间是否是钝角，即检测它们点积的结果 $q_{0} \cdot q_{1}$ 是否为负数。如果 $q_{0} \cdot q_{1} < 0$ ，那么我们就反转其中的一个四元数，比如说将 $q_{1}$ 改为 $-q_{1}$，并使用 $q_{0}$ 与 $-q_{1}$ 之间新的夹角来进行插值，这样才能保证插值的路径是最短的。

Squad

Slerp已经是我们理想中的插值方式了：它直接对角度插值，插值角度匀速变化，运算效率尚可。但是它还有一个小问题：角度变化的速率等于夹角，即 $\frac{d\theta_{t}}{dt} = \frac{d}{dt}(t\theta) = \theta$，这就意味着，当我们在多个角速度之间插值的时候，当在不同的四元数之间插值的时候，速率会发生突变，或者说在切断点处不可导。从数学上讲，函数 $f$ 连续并不意味着函数的一阶导连续（前者称为 $C^0$ 连续，后者称为 $C^1$ 连续）。

为此，我们希望能以牺牲固定角速度为条件，让插值的曲线能够在高阶导处也连续，下面介绍的Squad（Spherical and quadrangle）就是一种解决方法。

Bézier 曲线

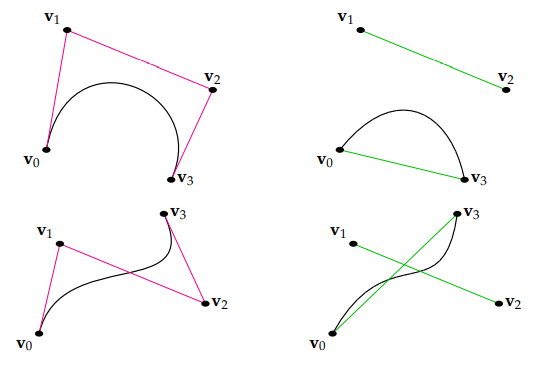
假设我们有一个向量的序列 $\pmb{v_{0}}$， $\pmb{v_{1}}$，$\dots$，$\pmb{v_{n}}$，如果我们想对这个序列进行插值，那么我们可以分别对每一对向量 $\pmb{v_{i}}$ 和 $\pmb{v_{i+1}}$ 进行插值，然后将插值的曲线连接起来，也就是我们所说的样条（Spline）．如果直接使用 Lerp 的话，我们会得到这样的结果（假设我们只有五个向量需要插值 $\pmb{v_{0}}$，$\pmb{v_{1}}$，$\pmb{v_{2}}$，$\pmb{v_{3}}$，$\pmb{v_{4}}$）：

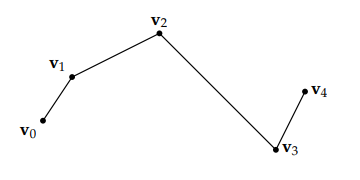
很明显，这个曲线虽然是连续的，但是它的一阶导数（切线）在切换插值向量时都不是连续的。为了解决这个问题，我们最常使用的就是 Bézier 曲线。我们一开始的想法可能会是将中间的 $\pmb{v_{1}}$，$\pmb{v_{2}}$，$\pmb{v_{3}}$ 作为控制点，直接使用一个四次 Bézier 曲线（因为有五个点）来生成这个近似曲线。但是 Bézier 曲线只会经过初始点与最终点（插值），一般不会经过中间的控制点（近似），所以这样求出来的曲线虽然是可导的，但是插值曲线不会经过中间的三个向量：

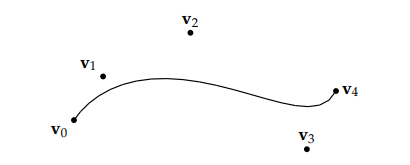
为了解决这个问题，我们可以分段对每两个向量 $\pmb{v_{i}}$ 和 $\pmb{v_{i+1}}$ 之间使用 Bézier曲线进行插值，之后将所有的曲线（样条）连接起来．因为我们需要让曲线的一阶导数（或者说曲线的趋势）连续，我们还需要知道它们的前一个向量 $\pmb{v_{i-1}}$ 和后一个向量 $\pmb{v_{i+2}}$，并且用它们生成两个控制点 $\pmb{s_{i}}$ 和 $\pmb{s_{i+1}}$ 来控制曲线的趋势．我们会使用 $\pmb{v_{i}}$ 和 $\pmb{v_{i+1}}$ 作为端点（曲线会经过这两个点），$\pmb{s_{i}}$ 和 $\pmb{s_{i+1}}$ 作为中间的控制点，使用一个三次 Bézier 曲线（Cubic Bézier Curve，四个点）来近似这个两个向量之间的插值。

在我们的例子中，因为我们一共有四对向量（$\pmb{v_{0}}\pmb{v_{1}}$、$\pmb{v_{1}}\pmb{v_{2}}$、$\pmb{v_{2}}\pmb{v_{3}}$、$\pmb{v_{3}}\pmb{v_{4}}$），我们会使用四个三次 Bézier 曲线对这五个点进行插值．我们知道，对于三次Bézier 曲线所产生的样条，如果想让最终的插值曲线达到 $C^1$ 连续，则需要让前一个样条在 $\pmb{v_{i}}$ 的控制点与当前样条在 $\pmb{v_{i}}$ 的控制点分别处于最终曲线在 $\pmb{v_{i}}$ 处切线对等的两侧：

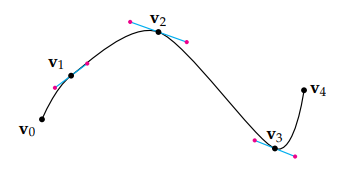
在上面的曲线中，蓝色的线就是曲线在点 $\pmb{v_{i}}$ 处的切线，红色的点就是三次 Bézier 曲线的控制点，分别处于切线对等的两侧．对于两个端点 $\pmb{v_{0}}$ 和 $\pmb{v_{4}}$，我们直接将这两个向量的控制点取为它们本身（这不是唯一的做法，但这样是可行的），最终得到一个平滑的曲线。我们希望将类似的逻辑带到四元数的超球面上，得到四元数序列的插值的方法，但在此之前我们需要了解如何构造一个三次 Bézier 曲线。

de Casteljau 算法

Bézier 曲线的构造有个著名的递归算法叫做 de Casteljau 算法（de Casteljau’s Algorithm），它对任意次方的 Bézier 曲线都是成立的，但是这里我们只关注三次 Bézier 曲线的情况。

这个算法最基本的思想就是线性插值的嵌套。假设我们有四个向量 $\pmb{v_{0}}$，$\pmb{v_{1}}$，$\pmb{v_{2}}$，$\pmb{v_{3}}$，那么我们可以这样子获得最终的三次 Bézier 曲线：

首先，我们对每一对向量 $\pmb{v_{0}}\pmb{v_{1}}$、$\pmb{v_{1}}\pmb{v_{2}}$、$\pmb{v_{2}}\pmb{v_{3}}$ 进行线性插值，获得 $\pmb{v_{01}}$、$\pmb{v_{12}}$、$\pmb{v_{23}}$：

$$
\pmb{v_{01}} = Lerp(\pmb{v_{0}}, \pmb{v_{1}}; t)\
\pmb{v_{12}} = Lerp(\pmb{v_{1}}, \pmb{v_{2}}; t)\
\pmb{v_{23}} = Lerp(\pmb{v_{2}}, \pmb{v_{3}}; t)\
$$

之后，我们对 $\pmb{v_{01}}\pmb{v_{12}}$ 和 $\pmb{v_{12}}\pmb{v_{23}}$ 这两对向量进行线性插值，获得 $\pmb{v_{012}}$ 和 $\pmb{v_{123}}$

$$
\pmb{v_{012}} = Lerp(\pmb{v_{01}}, \pmb{v_{12}}; t)\
\pmb{v_{123}} = Lerp(\pmb{v_{12}}, \pmb{v_{23}}; t)\
$$

最后，对 $\pmb{v_{012}}$ 和 $\pmb{v_{123}}$ 进行线性插值获得 $\pmb{v_{0123}}$，这个向量就是我们想要的最终结果，它就是三次 Bézier 曲线上的点：

$$
\pmb{v_{0123}} = Lerp(\pmb{v_{012}}, \pmb{v_{123}}; t)\
$$

虽然这个算法看起来很繁琐，但是我们可以通过一张图来理解它（取 $t$ = 0.4）：

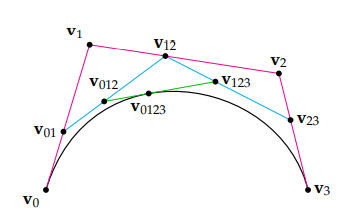
可以看到，虽然我们一直在使用线性插值，最终获得的却是一条三次 Bézier 曲线（黑色的线）。

如果将这些式子合并起来，我们就能得到三次 Bézier 曲线的递归公式。因为这个式子太长了，我将 $Lerp(\pmb{v_{i}}, \pmb{v_{i+1}}; t)$ 简写为 $L(\pmb{v_{i}}, \pmb{v_{i+1}}; t)$：
$$
Bézier(\pmb{v_{0}}, \pmb{v_{1}}, \pmb{v_{2}}, \pmb{v_{3}}; t) = L(L(L(\pmb{v_{0}}, \pmb{v_{1}}; t), L(\pmb{v_{1}}, \pmb{v_{2}}; t); t), L(L(\pmb{v_{1}}, \pmb{v_{2}}; t), L(\pmb{v_{2}}, \pmb{v_{3}}; t); t); t)
$$

如果将 Lerp 的定义 $Lerp(\pmb{v_{i}}, \pmb{v_{i+1}}; t) = (1 - t)\pmb{v_{i}} + t\pmb{v_{i+1}}$ 不断代入并展开的话，我们就能获得这样一个式子：
$$
Bézier(\pmb{v_{0}}, \pmb{v_{1}}, \pmb{v_{2}}, \pmb{v_{3}}; t) = (1 - t)^3\pmb{v_{0}} + 3(1 - t)^2t\pmb{v_{1}} + 3(1 - t)t^2\pmb{v_{2}} + t^3\pmb{v_{3}}
$$

因为每项的次数都是 3，所以我们说它是一个三次 Bézier 曲线。

我们可以直接将递归的公式运用到四元数上，得到四元数的球面 Bézier 曲线公式，但因为球面的线性插值不是 Lerp 而是 Slerp，我们需要将公式中所有的 Lerp 全部换成 Slerp（你可以想象一下，将四个向量形成的四边形看作是一个网格（Mesh），之后将这个网格贴在球面上）。同样因为公式太长，我会将 $Slerp(q_{i}, q_{i+1}; t)$ 简写为 $S(q_{i}, q_{i+1}; t)$：
$$
SBézier(q_{0}, q_{1}, q_{2}, q_{3}; t) = S(S(S(q_{0}, q_{1}; t), S(q_{1}, q_{2}; t);t),S(S(q_{1}, q_{2}; t), S(q_{2}, q_{3}; t); t); t)
$$
很明显这个方法实在是太复杂了。仅仅是一个 Slerp 就要使用四个三角函数，而我们这里一共有 7个 Slerp，如果真的要使用它进行插值会对性能产生非常大的影响。

Squad

三次 Bézier 曲线实际上是嵌套了三层一次（one-order）插值，而 Squad 则使用的是一层二次插值嵌套了一层一次插值。

我们首先是分别对 $\pmb{v_{0}}\pmb{v_{3}}$ 和 $\pmb{v_{1}}\pmb{v_{2}}$ 进行插值，得到 $\pmb{v_{03}}$ 和 $\pmb{v_{12}}$：
$$
\pmb{v_{03}} = Lerp(\pmb{v_{0}}, \pmb{v_{3}}; t)\
\pmb{v_{12}} = Lerp(\pmb{v_{1}}, \pmb{v_{2}}; t)\
$$
之后，我们使用 $2t(1 - t)$ 为参数，对 $\pmb{v_{03}}\pmb{v_{12}}$ 进行二次插值，得到最终的 $\pmb{v_{0312}}$ ：
$$
\pmb{v_{0312}} = Lerp(\pmb{v_{03}}, \pmb{v_{12}}; 2t(1 - t))\
$$

上述过程可以通过下图阐明（$t = 0.4$），黑色曲线就是生成的插值曲线：

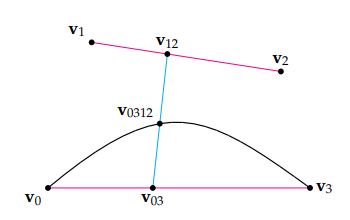
当然，我们也可以把它写成递归形式：
$$
Squad(\pmb{v_{0}}, \pmb{v_{1}}, \pmb{v_{2}}, \pmb{v_{3}}; t) = Lerp(Lerp(\pmb{v_{0}}, \pmb{v_{3}}; t), Lerp(\pmb{v_{1}}, \pmb{v_{2}}; t); 2t(1 - t))
$$

可以看到，这样的插值要比三次 Bézier 曲线简单很多，将七次 Lerp 减少到了三次．虽然最终的曲线与三次 Bézier 曲线不完全相同，但是已经很近似了。我们可以看几个对比。下图中，左边是三次 Bézier 曲线，右边是 Squad 曲线：

如果利用 Lerp 的定义 $Lerp(\pmb{v_{i}}, \pmb{v_{i+1}}; t) = (1 - t)\pmb{v_{i}} + t\pmb{v_{i+1}}$ 将递归式展开的话，我们能得到这样的式子
$$
Squad(\pmb{v_{0}}, \pmb{v_{1}}, \pmb{v_{2}}, \pmb{v_{3}}; t) = (2t^2 - 2t + 1)(1 - t)\pmb{v_{0}} + 2(1 - t)^2t\pmb{v_{1}} + 2(1 - t)t^2\pmb{v_{2}} + t(2t^2 - 2t + 1)\pmb{v_{3}}
$$

它仍是一个三次曲线，只不过系数有所不同。

如果我们将这个递归公式用于球面，就能得到四元数的 Squad 公式。
$$
Squad(q_{0}, q_{1}, q_{2}, q_{3}; t) = Slerp(Slerp(q_{0}, q_{3}; t), Slerp(q_{1}, q_{2}; t); 2t(1 - t))
$$

我们知道 $Slerp(q_{i}, q_{i+1}; t) = (q_{i+1}q_{i}^)^tq_{i}$，所以我们可以将 Squad 写成指数形式：
$$
Squad(q_{0}, q_{1}, q_{2}, q_{3}; t) = (Slerp(q_{1}, q_{2}; t)(Slerp(q_{0}, q_{3}; t))^)^{2t(1-t)}Slerp(q_{0}, q_{3}; t)
$$

Squad 应用

接下来，我们回到本章最初的主题，对多个单位四元数进行插值。如果我们有一个四元数序列 $q_{0}$，$q_{1}$，$\dots$，$q_{n}$，我们希望对每一对四元数 $q_{i}$ 和 $q_{i+1}$ 都使用 Squad 进行插值，所以我们有
$$
Squad(q_{i}, s_{i}, s_{i+1}, q_{i+1}; t) = Slerp(Slerp(q_{i}, q_{i+1}; t), Slerp(s_{i}, s_{i+1}; t); 2t(1 - t))
$$
现在，留下来的问题就是找出中间的控制点 $s_{i}$ 和 $s_{i+1}$ 了。类似于 Bézier 曲线的样条，我们同样需要前一个四元数 $q_{i-1}$ 以及 $q_{i+2}$ 的信息。

$s_{i}$ 的推导还是比较复杂的，但是它最基本的理念非常简单：让 Squad 在切换点可导，从而达到 $C^1$ 连续。也就是说，我们希望 $q_{i-1}q_{i}$ 插值时在 $t = 1$ 处的导数，与 $q_{i}q_{i+1}$ 插值时在 $t = 0$ 处的导数相等：
$$
Squad’(q_{i-1}, s_{i-1}, s_{i}, q_{i}; 1) = Squad’(q_{i}, s_{i}, s_{i+1}, q_{i+1}; 0)
$$

如果我们想要从这里继续推导下去的话，就需要用到单位四元数导数的定义（它和 $q = [\cos(\theta), \sin(\theta)\pmb{u}] = e^{u\theta}$ 有关）。最终得到
$$
s_{i} = q_{i}exp(-\frac{\log(q_{i}^*q_{i-1}) + \log(q_{i}^*q_{i+1})}{4})
$$
注意，和 Bézier 曲线的样条不同的是，这里的 $s_{i}$ 在对 $q_{i-1}q_{i}$ 插值时和对 $q_{i}q_{i+1}$ 插值时都是相同的，不像之前是处于切线的两端不同的两个向量。

与两个四元数之间的插值一样，Squad 同样会受到双重覆盖的影响。我们在计算中间控制点和插值之前，需要先选中一个四元数，比如说 $q_{i}$，检测它与其它三个四元数之间的夹角，如果是钝角就翻转，将插值的路线减到最小。