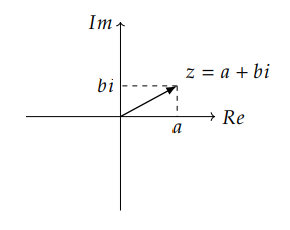四元数和三维旋转(一)

由于使用欧拉角进行旋转时会存在万向锁的问题，同时，用欧拉角进行插值也不尽方便，而基于四元数的旋转既解决了万向锁的问题，又能非常方便地进行插值。本文将对在学习过程中遇到的四元数的定义、推导、性质、插值等问题进行总结归纳。

复数

我们先来简要讨论一下复数的一些性质以及它与 2D 旋转之间的关系，四元数的很多性质都与复数非常类似，所以理解复数的一些性质对理解四元数非常有帮助。

定义

任意一个复数 $z \in \mathbb{C}$ 都可以表示为 $z = a + bi$ 的形式，其中 $a,b \in \mathbb{R}$ 而且 $i^2 = -1$。我们将 $a$ 称为复数 $z$ 的实部，表示为 $a = Re(z)$，$b$ 称为复数 $z$ 的虚部，表示为 $b = Im(z)$。

因为 $z = a + bi$ 其实就是对于 ${1, i}$ 这个基（Basis）的线性组合（Linear Combination），我们也可以用向量来表示一个复数：
$$
z = \begin{bmatrix}
a\
b\
\end{bmatrix}
$$

因为这个向量有两个元素，我们可以使用复平面上的一个点来表示一个复数。复平面的横坐标代表它的实部，纵坐标代表它的虚部：

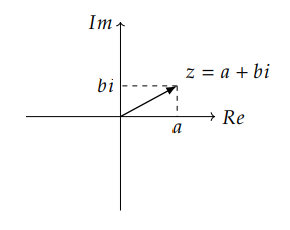
复数的加减法

如果我们有两个复数 $z_{1} = a + bi$，$z_{2} = c + di$，它们的和就是分量相加的结果：
$$
z_{1} + z_{2} = (a + c) + (b + d)i
$$
同理，如果要对它们相减，直接将分量相减就可以了。
$$
z_{1} - z_{2} = (a - c) + (b - d)i
$$

复数的乘法

如果有两个复数 $z_{1} = a + bi$，$z_{2} = c + di$，我们可以使用分配律来计算它们的乘积
$$
\begin{aligned}
z_{1}z_{2} &= (a + bi)(c + di)\
&= ac + adi + bci + bdi^2\
&= ac - bd + adi +bci\
&= a\textcolor{red}{c} - b\textcolor{blue}{d} +\
&\quad(b\textcolor{red}{c} + a\textcolor{blue}{d})i
\end{aligned}
$$
如果仔细观察可以发现，复数相乘的结果其实也是一个矩阵与向量相乘的结果，也就是说：
$$
\begin{aligned}
z_{1}z_{2} &= a\textcolor{red}{c} - b\textcolor{blue}{d} +\
&\quad(b\textcolor{red}{c} + a\textcolor{blue}{d})i\
&=
\begin{bmatrix}
a&-b\
b&a\
\end{bmatrix}
\begin{bmatrix}
\textcolor{red}{c}\
\textcolor{blue}{d}\
\end{bmatrix}
\end{aligned}
$$

右侧的 $\begin{bmatrix}c\ d \end{bmatrix}$ 是用向量的形式来表示的 $z_{2}$，而左侧的 $\begin{bmatrix} a&-b\ b&a\ \end{bmatrix}$ 则是 $z_{1}$ 的矩阵形式。我们可以发现，复数相乘这个运算，其实是与 $\begin{bmatrix} a&-b\ b&a\ \end{bmatrix}$ 则是 $z_{1}$ 这个矩阵所代表的变换是等价的。

那么在矩阵形式下，复数与复数的相乘也可以表示为矩阵的相乘，如果我们有两个复数 $z_{1} = a + bi$，$z_{2} = c + di$，那么与 $z_{1}z_{2}$ 所代表的变换则可以表示为

$$
\begin{aligned}
z_{1}z_{2} &=
\begin{bmatrix}
a&-b\
b&a\
\end{bmatrix}
\begin{bmatrix}
c&-d\
d&c\
\end{bmatrix}\
&=
\begin{bmatrix}
ac - bd&-(bc + ad)\
bc + ad&ac - bd\
\end{bmatrix}
\end{aligned}
$$

复数的相乘满足交换律，即 $z_{1}z_{2}$ 与 $z_{2}z_{1}$ 是等价的

$$
\begin{aligned}
z_{2}z_{1} &=
\begin{bmatrix}
c&-d\
d&c\
\end{bmatrix}
\begin{bmatrix}
a&-b\
b&a\
\end{bmatrix}\
&=
\begin{bmatrix}
ac - bd&-(bc + ad)\
bc + ad&ac - bd\
\end{bmatrix} = z_{1}z_{2}
\end{aligned}
$$

除此之外，我们来看一下一些特殊的矩阵形式：
$$
1 = \begin{bmatrix}
1&0\
0&1\
\end{bmatrix}
= I
\quad(a = 1, b = 0)
$$
$$
i = \begin{bmatrix}
0&-1\
1&0\
\end{bmatrix}
\quad(a = 0, b = 1)
$$

实数单位 1 与矩阵单位矩阵是等价的，而虚数单位 $i$ 则等价于 $\begin{bmatrix} 0&-1\ 1&0\ \end{bmatrix}$，如果我们尝试对它进行平方，可以发现：

$$
i^2 = i \cdot i =
\begin{bmatrix}
0&-1\
1&0\
\end{bmatrix}
\begin{bmatrix}
0&-1\
1&0\
\end{bmatrix}
= \begin{bmatrix}
-1&0\
0&-1\
\end{bmatrix} = -I = -1
$$

即便实在矩阵形式下，$i^2$ 与 -1 其实也是等价的，这进一步展示了复数与这一矩阵形式的关联。

复数的模长与共轭

复数 $z = a + bi$ 的模长（Magnitude）定义为
$$
\lVert z \rVert = \sqrt{a^2 + b^2}
$$

复数 $z = a + bi$ 的共轭（Conjugate）定义为

$$
\bar{z} = a - bi
$$

如果尝试计算 $z\bar{z}$，我们就会发现

$$
\begin{aligned}
z\bar{z} &= (a + bi)(a - bi)\
&= a^2 - abi + abi + b^2\
&= a^2 + b^2 = {\lVert z \rVert}^2
\end{aligned}
$$

所以，一个复数的模长又可以通过下面的方式计算

$$
\lVert z \rVert = \sqrt{z\bar{z}}
$$

复数与二维旋转

注意观察复数 $z$ 的矩阵形式 $\begin{bmatrix} a&-b\ b&a\ \end{bmatrix}$，我们可以把它变换为下述形式：

$$
\begin{bmatrix} a&-b\ b&a\ \end{bmatrix} = \sqrt{a^2 + b^2}
\begin{bmatrix}
\frac{a}{\sqrt{a^2 + b^2}}&\frac{-b}{\sqrt{a^2 + b^2}}\
\frac{b}{\sqrt{a^2 + b^2}}&\frac{a}{\sqrt{a^2 + b^2}}\
\end{bmatrix}
$$

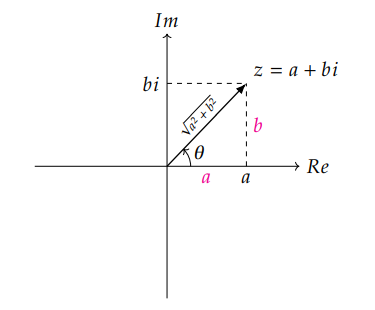
可以看到，$\lVert z \rVert$ 正是复数 $z$ 与坐标轴所形成的三角形的斜边长，而 $a$，$b$ 分别为三角形的两个直角边．如果将斜边与实数轴正方向的夹角记为 $\theta$ 的话，按照三角函数的定义可以得出 $\frac{a}{\sqrt{a^2 + b^2}} = \cos(\theta)$ 且 $\frac{b}{\sqrt{a^2 + b^2}} = \sin(\theta)$,这个角度 $\theta$ 其实就是 $atan2(b, a)$。知道了这些，原矩阵就可以变形为

$$
\begin{aligned}
\begin{bmatrix} a&-b\ b&a\ \end{bmatrix} &= \sqrt{a^2 + b^2}
\begin{bmatrix}
\cos(\theta)&-\sin(\theta)\
\sin(\theta)&\cos(\theta)\
\end{bmatrix}\
&= \lVert z \rVert
\begin{bmatrix}
\cos(\theta)&-\sin(\theta)\
\sin(\theta)&\cos(\theta)\
\end{bmatrix}\
&= \lVert z \rVert \cdot I
\begin{bmatrix}
\cos(\theta)&-\sin(\theta)\
\sin(\theta)&\cos(\theta)\
\end{bmatrix}\
&= \begin{bmatrix}
\lVert z \rVert&0\
0&\lVert z \rVert\
\end{bmatrix}
\begin{bmatrix}
\cos(\theta)&-\sin(\theta)\
\sin(\theta)&\cos(\theta)\
\end{bmatrix}\
\end{aligned}
$$

其中，左边的 $\begin{bmatrix}\lVert z \rVert&0\ 0&\lVert z \rVert\ \end{bmatrix}$ 是缩放矩阵，而右边的 $\begin{bmatrix}\cos(\theta)&-\sin(\theta)\ \sin(\theta)&\cos(\theta)\ \end{bmatrix}$ 是 2D 旋转矩阵。

让我们看看这个矩阵对两个基 $\begin{bmatrix}1\ 0 \end{bmatrix}$ 和 $\begin{bmatrix}0\ 1 \end{bmatrix}$ 的变换效果，首先是 $\begin{bmatrix}1\ 0 \end{bmatrix}$:

$$
\begin{aligned}
\begin{bmatrix}
a&-b\
b&a\
\end{bmatrix}
\begin{bmatrix}
1\
0\
\end{bmatrix}
&= \begin{bmatrix}
\lVert z \rVert&0\
0&\lVert z \rVert\
\end{bmatrix}
\begin{bmatrix}
\cos(\theta)&-\sin(\theta)\
\sin(\theta)&\cos(\theta)\
\end{bmatrix}
\begin{bmatrix}
1\
0\
\end{bmatrix}\
&= \begin{bmatrix}
\lVert z \rVert&0\
0&\lVert z \rVert\
\end{bmatrix}
\begin{bmatrix}
\cos(\theta)\
\sin(\theta)\
\end{bmatrix}
\end{aligned}
$$

第一步首先将 $\begin{bmatrix}1\ 0 \end{bmatrix}$ 变换到了 $\begin{bmatrix}\cos(\theta)\ \sin(\theta) \end{bmatrix}$ 的位置，也就是逆时针旋转了 $\theta$ 度，接下来
$$
\begin{bmatrix}
\lVert z \rVert&0\
0&\lVert z \rVert\
\end{bmatrix}
\begin{bmatrix}
\cos(\theta)\
\sin(\theta)\
\end{bmatrix} =
\begin{bmatrix}
\lVert z \rVert\cos(\theta)\
\lVert z \rVert\sin(\theta)\
\end{bmatrix}
$$
缩放矩阵将 $\begin{bmatrix}\cos(\theta)\ \sin(\theta)\ \end{bmatrix}$ 缩放了 $\lVert z \rVert$ 倍，变为 $\begin{bmatrix}\lVert z \rVert\cos(\theta)\ \lVert z \rVert\sin(\theta)\ \end{bmatrix}$。总的来说，就是对 $\begin{bmatrix}1\ 0 \end{bmatrix}$ 旋转了 $\theta$ 度，并缩放了 $\lVert z \rVert$ 倍。

接下来是 $\begin{bmatrix}0\ 1 \end{bmatrix}$：

$$
\begin{aligned}
\begin{bmatrix}
a&-b\
b&a\
\end{bmatrix}
\begin{bmatrix}
0\
1\
\end{bmatrix}
&= \begin{bmatrix}
\lVert z \rVert&0\
0&\lVert z \rVert\
\end{bmatrix}
\begin{bmatrix}
\cos(\theta)&-\sin(\theta)\
\sin(\theta)&\cos(\theta)\
\end{bmatrix}
\begin{bmatrix}
0\
1\
\end{bmatrix}\
&= \begin{bmatrix}
\lVert z \rVert&0\
0&\lVert z \rVert\
\end{bmatrix}
\begin{bmatrix}
-\sin(\theta)\
\cos(\theta)\
\end{bmatrix}
\end{aligned}
$$

这里，第一步将 $\begin{bmatrix}0\ 1 \end{bmatrix}$ 变换到了 $\begin{bmatrix}-\sin(\theta)\ \cos(\theta) \end{bmatrix}$ 的位置，这同样是逆时针旋转了 $\theta$ 度，见下图：

第二步变换同样会将 $\begin{bmatrix}-\sin(\theta)\ \cos(\theta) \end{bmatrix}$ 缩放为 $\begin{bmatrix}-\lVert z \rVert\sin(\theta)\ \lVert z \rVert\cos(\theta) \end{bmatrix}$。这样等于是将整个坐标系逆时针旋转了 $\theta$ 度，并缩放了 $\lVert z \rVert$ 倍。

换句话说，复数相乘的几何意义就是旋转与缩放变换的复合。如果有一个复数 $z = a + bi$，那么 $z$ 与任意一个复数 $c$ 相乘都会将 $c$ 逆时针旋转 $\theta = atan2(b, a)$ 度，并将其缩放 $\lVert z \rVert = \sqrt{a^2 + b^2}$ 倍。

如果复数的模长为 1，那么它的几何意义就只有旋转。

$$
z = \begin{bmatrix}
\cos(\theta)&-\sin(\theta)\
\sin(\theta)&\cos(\theta)\
\end{bmatrix}
$$

如果我们想让 2D 空间中任意一个向量 $\vec{v}$ 旋转 $\theta$ 度，那么我们就可以使用这个矩阵对 $\vec{v}$ 进行变换：

Theorem 1：2D 旋转公式（矩阵型）
$$
\vec{v’} = \begin{bmatrix}
\cos(\theta)&-\sin(\theta)\
\sin(\theta)&\cos(\theta)\
\end{bmatrix}
\vec{v}
$$

其实 $\begin{bmatrix}\cos(\theta)&-\sin(\theta)\ \sin(\theta)&\cos(\theta)\ \end{bmatrix}$ 这个旋转矩阵如果写成复数形式的话就是 $\cos(\theta) + i\sin(\theta)$

如果我们将向量 $\vec{v} = \begin{bmatrix} x\ y\ \end{bmatrix}$ 看作是一个复数 $v = x + yi$，其中实部为 $x$，虚部为 $y$。那么我们可以构造一个复数 $z = \cos(\theta) + i\sin(\theta)$，并将它与 $v$ 相乘来进行旋转，旋转 $\theta$ 度之后的向量 $v’$ 可以用等价的复数乘法来表示：

Theorem 2：2D 旋转公式（复数积型）
$$
\begin{aligned}
v’ &= zv\
&= (\cos(\theta) + i\sin(\theta)) v
\end{aligned}
$$

复数的极坐标型

$\cos(\theta) + i\sin(\theta)$ 还可以进行下一步的变形，根据欧拉公式（Euler’s Formula），
$$
\cos(\theta) + i\sin(\theta) = e^{i\theta}
$$

欧拉公式的证明：

令 $f(\theta) = \frac{\cos(\theta) + i\sin(\theta)}{e^{i\theta}} = e^{-i\theta}(\cos(\theta) + i\sin(\theta))$，对实数 $\theta$，对 $f(\theta)$ 求导，得到 $f’(\theta) = e^{-i\theta}(i\cos(\theta) - \sin(\theta)) - ie^{-i\theta}(\cos(\theta) + i\sin(\theta)) = 0$，因此 $f(\theta)$ 是常数。又因为 $f(0) = 1$，所以 $f(\theta) \equiv 1$。欧拉公式得证。

有了这个等式，我们就能将复数表示为
$$
\begin{aligned}
z &= \lVert z \rVert
\begin{bmatrix}
\cos(\theta)&-\sin(\theta)\
\sin(\theta)&\cos(\theta)\
\end{bmatrix}
&= \lVert z \rVert (\cos(\theta) + i\sin(\theta))
&= \lVert z \rVert e^{i\theta}
\end{aligned}
$$

如果我们定义 $r = \lVert z \rVert$，我们就得到了复数的极坐标形式：
$$
z = re^{i\theta}
$$

现在复数的定义就与实部与虚部的两个分量 $a$，$b$ 无关了，我们可以使用一个缩放因子 $r$ 和旋转角度 $\theta$ 的形式来定义任意一个复数，而且它旋转与缩放的性质仍然存在。如果我们想对 2D 空间中的向量 $\vec{v} = \begin{bmatrix} x\ y\ \end{bmatrix}$ 进行旋转并缩放，我们可以类似地将这个向量看作是一个复数 $v = x + yi$，那么，经过旋转 $\theta$ 度，缩放 $r$ 倍之后的向量 $v’$ 就可以这样计算：
$$
v’ = re^{i\theta}v
$$
如果仅需要旋转 $\theta$ 度的话，可以令缩放因子 $r = 1$，那么变换后的结果就是

Theorem 3：2D 旋转公式（指数型）
$$
v’ = e^{i\theta}v
$$

复数的几种表示形式总结

• 代数形式一：$z = a + bi$
• 代数形式二：$z = r(\cos(\theta) + i\sin(\theta))$
• 向量形式：$z = \begin{bmatrix}a\ b\ \end{bmatrix}$
• 矩阵形式一：$\begin{bmatrix} a&-b\ b&a\ \end{bmatrix}$
• 矩阵形式二：$\begin{bmatrix}\lVert z \rVert&0\ 0&\lVert z \rVert\ \end{bmatrix} \begin{bmatrix}\cos(\theta)&-\sin(\theta)\ \sin(\theta)&\cos(\theta)\ \end{bmatrix}\$
• 极坐标形式：$z = re^{i\theta}$

这几种形式完全等价

旋转的复合

如果我们有两个代表 2D 旋转的单位复数 $z_{1} = \cos(\theta) + i\sin(\theta)$，$z_{2} = \cos(\phi) + i\sin(\phi)$ 以及一个向量 $v = x + yi$，我们可以先对 $v$ 进行 $z_{1}$ 的旋转
$$
v’ = z_{1}v
$$
在此基础上，我们对 $v’$ 进行 $z_{2}$ 的旋转
$$
\begin{aligned}
v’’ &= z_{2}(z_{1}v)\
&= (z_{2}z_{1})v
\end{aligned}
$$
如果我们将这两次旋转所作出的等效变换称为 $z_{net}$，那么
$$
\begin{aligned}
v’’ &= (z_{2}z_{1})v = z_{net}v\
z_{net} &= z_{2}z_{1}
\end{aligned}
$$

因为复数的相乘遵守交换律，所以
$$
z_{net} = z_{2}z_{1} = z_{1}z_{2}
$$
如果尝试计算一下 $z_{net}$，会发现
$$
\begin{aligned}
z_{net} &= (\cos(\theta) + i\sin(\theta))(\cos(\phi) + i\sin(\phi))\
&= \cos(\theta)\cos(\phi) + i(\cos(\theta)\sin(\phi)) + i(\sin(\theta)\cos(\phi)) - \sin(\theta)\sin(\phi)\
&= (\cos(\theta)\cos(\phi) - \sin(\theta)\sin(\phi)) + (\cos(\theta)\sin(\phi) + \sin(\theta)\cos(\phi))i
\end{aligned}
$$

这个式子可以利用三角恒等式化简为：
$$
\begin{aligned}
z_{net} &= (\cos(\theta) + i\sin(\theta))(\cos(\phi) + i\sin(\phi))\
&= \cos(\theta + \phi) + i\sin(\theta + \phi)
\end{aligned}
$$

所以，当我们对两个 2D 旋转进行复合时，所得到的变换 $z_{net}$ 仍是一个旋转，而且与施加的次序无关。这个等效变换的旋转角是 $z_{1} 与 $z_{2} 旋转角之和。

轴角式旋转

假设我们有一个经过原点的（如果旋转轴不经过原点我们可以先将旋转轴平移到原点，进行旋转，再平移回原处）旋转轴 $\vec{u} = (x,y,z)^T$，我们希望将一个向量 $\vec{v}$，沿着这个旋转轴旋转 $\theta$ 度，变换到 $\vec{v’}$

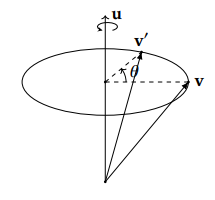
我们使用右手坐标系统，并且将使用右手定则来定义旋转的正方向。你可以将右手拇指指向旋转轴 $\vec{u}$ 的正方向，这时其他四个手指弯曲的方向即为旋转的正方向。在上图中即为逆时针方向。

为了消除旋转轴 $\vec{u}$ 模长这个多余的自由度，我们可以规定 $\vec{u}$ 的模长为 1，即 $\vec{u}$ 是一个单位向量。规定 $\vec{u}$ 为单位向量后能为我们带来很多便利，这也是数学和物理中对方向定义的惯例。如果 $\vec{u}$ 不是一个单位向量，我们可以通过下面的公式将它转化为一个单位向量
$$
\hat{u} = \frac{\vec{u}}{\lVert \vec{u} \rVert}
$$

旋转的分解

我们可以将 $\vec{v}$ 分解为平行于旋转轴 $\vec{u}$ 以及正交于 $\vec{u}$ 的两个分量，$\vec{v_{\parallel}}$ 和 $\vec{v_{\perp}}$，即
$$
\vec{v} = \vec{v_{\parallel}} + \vec{v_{\perp}}
$$
我们可以分别旋转这两个分量，再将它们旋转的结果相加获得旋转后的向量
$$
\vec{v’} = \vec{v_{\parallel}‘} + \vec{v_{\perp}’}
$$
下面是分解的示意图：

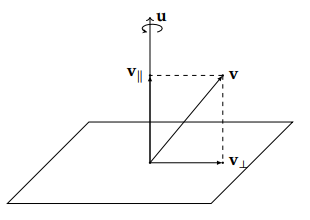
可以看到，$\vec{v_{\parallel}}$ 其实就是 $\vec{v}$ 在 $\vec{u}$ 上的正交投影，根据正交投影公式，我们可以得出：

$$
\begin{aligned}
\vec{v_{\parallel}} &= proj_{u}(\vec{v})\
&= \frac{\vec{u}\cdot\vec{v}}{\vec{u}\cdot\vec{u}}\vec{u}\
&= \frac{\vec{u}\cdot\vec{v}}{\lVert \vec{u} \rVert ^2}\vec{u}\
&= (\vec{u}\cdot\vec{v})\vec{u}
\end{aligned}
$$

因为 $\vec{v} = \vec{v_{\parallel}} + \vec{v_{\perp}}$，我们可以得到
$$
\begin{aligned}
\vec{v_{\perp}} &= \vec{v} - \vec{v_{\parallel}}\
&= \vec{v} - (\vec{u}\cdot\vec{v})\vec{u}
\end{aligned}
$$

$\vec{v_{\parallel}}$ 的旋转

从之前的图示中可以看到，$\vec{v_{\parallel}}$ 其实没有被旋转，仍然与旋转轴 $\vec{u}$ 重合，所以

Theorem 4：3D 旋转公式（向量型，平行情况）
当 $\vec{v_{\parallel}}$ 平行于旋转轴 $\vec{u}$ 时，旋转 $\theta$ 角度之后的 $\vec{v_{\parallel}‘}$ 为：
$$
\vec{v_{\parallel}’} = \vec{v_{\parallel}}
$$

$\vec{v_{\perp}}$ 的旋转

接下来，我们需要处理正交于 $\vec{u}$ 的 $\vec{v_{\perp}}$。因为这两个向量是正交的，这个旋转可以看作是平面内的一个旋转。因为旋转不改变 $\vec{v_{\perp}}$ 的长度，所以路径是一个园。下面是这个旋转的示意图，右侧的为俯视图：

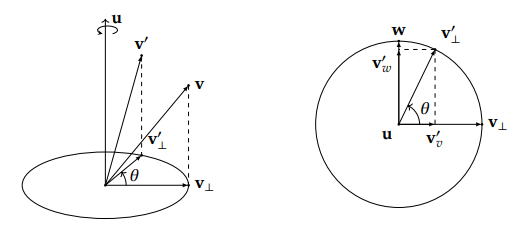
现在，3D 的旋转就被我们转化为了 2D 平面上的旋转，由于在这个平面上我们只有一个向量 $\vec{v_{\perp}}$，用它来表示一个旋转是不够的，我们还需构造一个同时正交于 $\vec{u}$ 和 $\vec{v_{\perp}}$ 的向量 $\vec{w}$，这个可以通过叉乘来获得
$$
\vec{w} = \vec{u}\times\vec{v_{\perp}}
$$

注意叉乘的顺序，因为我们使用的是右手坐标系统，按右手定则这个新的向量 $\vec{w}$ 指向 $\vec{v_{\perp}}$ 逆时针旋转 $\pi / 2$ 后的方向，并且和 $\vec{v_{\perp}}$ 一样也处于正交于 $\vec{u}$ 的平面内，因为 $\lVert\vec{u}\rVert = 1$，我们可以发现：
$$
\begin{aligned}
\lVert\vec{w}\rVert &= \lVert\vec{u}\times\vec{v_{\perp}}\rVert\
&= \lVert\vec{u}\rVert\cdot\lVert\vec{v_{\perp}}\rVert\cdot\sin(\pi/2)\
&= \lVert\vec{v_{\perp}}\rVert
\end{aligned}
$$
$\vec{w}$ 和 $\vec{v_{\perp}}$ 的模长相同，且 $\vec{w}$ 也位于圆上，我们可以将 $\vec{w}$ 和 $\vec{v_{\perp}}$ 作为平面内的两个坐标轴，我们现在可以把 $\vec{v_{\perp}‘}$ 投影到 $\vec{w}$ 和 $\vec{v_{\perp}}$ 上，将其分解为 $\vec{v_{v}’}$ 和 $\vec{v_{w}'}$，利用三角形的知识我们可以得到：

$$
\begin{aligned}
\vec{v_{\perp}‘} &= \vec{v_{v}’} + \vec{v_{w}'}\
&= \cos(\theta)\vec{v_{\perp}} + \sin(\theta)\vec{w}\
&= \cos(\theta)\vec{v_{\perp}} + \sin(\theta)(\vec{u}\times\vec{v_{\perp}})
\end{aligned}
$$

Theorem 5：3D 旋转公式（向量型，正交情况）
当 $\vec{v_{\perp}}$ 正交于旋转轴 $\vec{u}$ 时，旋转 $\theta$ 角度之后的 $\vec{v_{\perp}‘}$ 为：
$$
\vec{v_{\perp}’} = \cos(\theta)\vec{v_{\perp}} + \sin(\theta)(\vec{u}\times\vec{v_{\perp}})
$$

$\vec{v}$ 的旋转

将上面两个结果组合可以获得：
$$
\begin{aligned}
\vec{v’} &= \vec{v_{\parallel}‘} + \vec{v_{\perp}’}\
&= \vec{v_{\parallel}} + \cos(\theta)\vec{v_{\perp}} + \sin(\theta)(\vec{u}\times\vec{v_{\perp}})
\end{aligned}
$$

因为叉乘遵守分配律，
$$
\begin{aligned}
\vec{u}\times\vec{v_{\perp}} &= \vec{u}\times(\vec{v} - \vec{v_{\parallel}})\
&= \vec{u}\times\vec{v} - \vec{u}\times\vec{v_{\parallel}}\
&= \vec{u}\times\vec{v}\quad (\vec{u} 平行于 \vec{v_{\parallel}}，所以 \vec{u}\times\vec{v_{\parallel}} = \vec{0})
\end{aligned}
$$

最后，将 $\vec{v_{\parallel}} = (\vec{u}\cdot\vec{v})\vec{u}$ 和 $\vec{v_{\perp}} = \vec{v} - (\vec{u}\cdot\vec{v})\vec{u}$ 代入
$$
\begin{aligned}
\vec{v’} &= (\vec{u}\cdot\vec{v})\vec{u} + \cos(\theta)(\vec{v} - (\vec{u}\cdot\vec{v})\vec{u}) + \sin(\theta)(\vec{u}\times\vec{v})\
&= \cos(\theta)\vec{v} + (1 - \cos(\theta))(\vec{u}\cdot\vec{v})\vec{u} + \sin(\theta)(\vec{u}\times\vec{v})
\end{aligned}
$$
这样我们就得到了一般形式的旋转公式：

Theorem 6：3D 旋转公式（向量型，一般情况）
3D 空间中任意一个 $\vec{v}$ 沿着单位向量 $\vec{u}$ 旋转 $\theta$ 角度之后的 $\vec{v_{\perp}‘}$ 为：
$$
\vec{v’} = \cos(\theta)\vec{v} + (1 - \cos(\theta))(\vec{u}\cdot\vec{v})\vec{u} + \sin(\theta)(\vec{u}\times\vec{v})
$$