本文最后更新于:2025年4月17日 晚上
三角形
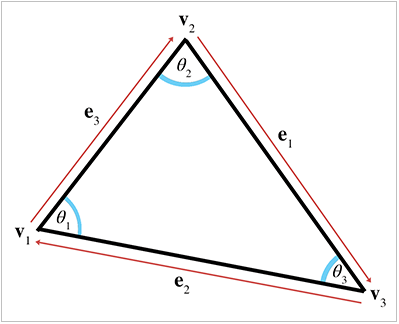
想要定义一个三角形只需列出其 3 个顶点即可,但是列出这三个顶点的顺序非常重要。在左手坐标系并且从三角形正面看时,通常按照顺时针顺序枚举顶点。我们将这 3 个顶点分别称为 v 1 \bf v_1 v 1 v 2 \bf v_2 v 2 v 3 \bf v_3 v 3
其中的边长和长度可以表示为:
e 1 = v 3 − v 2 e 2 = v 1 − v 3 e 3 = v 2 − v 1 l 1 = ∥ e 1 ∥ l 2 = ∥ e 2 ∥ l 3 = ∥ e 3 ∥ \begin{aligned}
{\bf e_1} &= {\bf v_3} - {\bf v_2} & {\bf e_2} &= {\bf v_1} - {\bf v_3} & {\bf e_3} &= {\bf v_2} - {\bf v_1}\\
l_1 &= \lVert {\bf e_1} \rVert & l_2 &= \lVert {\bf e_2} \rVert & l_3 &= \lVert {\bf e_3} \rVert
\end{aligned}
e 1 l 1 = v 3 − v 2 = ∥ e 1 ∥ e 2 l 2 = v 1 − v 3 = ∥ e 2 ∥ e 3 l 3 = v 2 − v 1 = ∥ e 3 ∥
正弦定理:
sin ( θ 1 ) l 1 = sin ( θ 2 ) l 2 = sin ( θ 3 ) l 3 \frac{\sin(\theta_1)}{l_1} = \frac{\sin(\theta_2)}{l_2} = \frac{\sin(\theta_3)}{l_3}
l 1 sin ( θ 1 ) = l 2 sin ( θ 2 ) = l 3 sin ( θ 3 )
余弦定理:
l 1 2 = l 2 2 + l 3 2 − 2 l 2 l 3 cos θ 1 l 2 2 = l 1 2 + l 3 2 − 2 l 1 l 3 cos θ 2 l 3 2 = l 1 2 + l 2 2 − 2 l 1 l 2 cos θ 3 \begin{aligned}
l_1^2 = l_2^2 + l_3^2 - 2l_2l_3\cos\theta_1\\
l_2^2 = l_1^2 + l_3^2 - 2l_1l_3\cos\theta_2\\
l_3^2 = l_1^2 + l_2^2 - 2l_1l_2\cos\theta_3\\
\end{aligned}
l 1 2 = l 2 2 + l 3 2 − 2 l 2 l 3 cos θ 1 l 2 2 = l 1 2 + l 3 2 − 2 l 1 l 3 cos θ 2 l 3 2 = l 1 2 + l 2 2 − 2 l 1 l 2 cos θ 3
三角形周长:
p = l 1 + l 2 + l 3 p = l_1 + l_2 + l_3
p = l 1 + l 2 + l 3
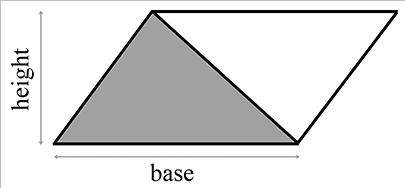
三角形面积
三角形面积:
A = b h / 2 A = bh/2
A = bh /2
如果高度未知,则可以使用海伦公式,该公式只需要三边的边长即可求三角形的面积:
s = l 1 + l 2 + l 3 2 = p 2 A = s ( s − l 1 ) ( s − l 2 ) ( s − l 3 ) \begin{aligned}
s = \frac{l_1 + l_2 + l_3}{2} = \frac{p}{2}
A = \sqrt{s(s - l_1)(s - l_2)(s - l_3)}
\end{aligned}
s = 2 l 1 + l 2 + l 3 = 2 p A = s ( s − l 1 ) ( s − l 2 ) ( s − l 3 )
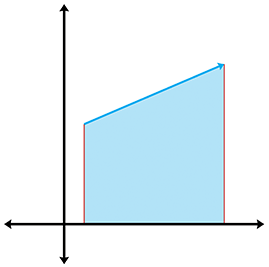
我们还可以单独通过顶点坐标来计算三角形的面积,其基本思想是,为三角形的三条边中的每一条边计算梯形的有符号的面积,该面积由边和下方的 x 轴所界定,如下图所示
“有符号的面积”是指如果边的指向是从左到右,则该面积为正;如果边的指向是从右到左,则面积为负。请注意,无论三角形如何定向,总会有至少一条边的面积为正值并且至少一条边的面积为负值。垂直边的面积为零。每条边下的面积公式为:
A ( e 1 ) = ( y 3 + y 2 ) ( x 3 − x 2 ) 2 A ( e 2 ) = ( y 1 + y 3 ) ( x 1 − x 3 ) 2 A ( e 3 ) = ( y 2 + y 1 ) ( x 2 − x 1 ) 2 \begin{aligned}
A({\bf e_1}) = \frac{(y_3 + y_2)(x_3 - x_2)}{2}\\
A({\bf e_2}) = \frac{(y_1 + y_3)(x_1 - x_3)}{2}\\
A({\bf e_3}) = \frac{(y_2 + y_1)(x_2 - x_1)}{2}\\
\end{aligned}
A ( e 1 ) = 2 ( y 3 + y 2 ) ( x 3 − x 2 ) A ( e 2 ) = 2 ( y 1 + y 3 ) ( x 1 − x 3 ) A ( e 3 ) = 2 ( y 2 + y 1 ) ( x 2 − x 1 )
通过对 3 个梯形的有符号面积求和,可以获得三角形本身的面积。假设三角形周围的顶点按顺时针排序(如果按相反的顺序排序会反转面积的符号),可以通过下式对梯形的面积求和来计算三角形的有符号面积:
A = A ( e 1 ) + A ( e 2 ) + A ( e 3 ) = ( y 3 + y 2 ) ( x 3 − x 2 ) + ( y 1 + y 3 ) ( x 1 − x 3 ) + ( y 2 + y 1 ) ( x 2 − x 1 ) 2 = y 3 x 3 − y 3 x 2 + y 2 x 3 − y 2 x 2 + y 1 x 1 − y 1 x 3 + y 3 x 1 − y 3 x 3 + y 2 x 2 − y 2 x 1 + y 1 x 2 − y 1 x 1 2 = − y 3 x 2 + y 2 x 3 − y 1 x 3 + y 3 x 1 − y 2 x 1 + y 1 x 2 2 = y 1 ( x 2 − x 3 ) + y 2 ( x 3 − x 1 ) + y 3 ( x 1 − x 2 ) 2 \begin{aligned}
A &= A({\bf e_1}) + A({\bf e_2}) + A({\bf e_3})\\
&= \frac{(y_3 + y_2)(x_3 - x_2) + (y_1 + y_3)(x_1 - x_3) + (y_2 + y_1)(x_2 - x_1)}{2}\\
&= \frac{y_3x_3 - y_3x_2 + y_2x_3 - y_2x_2 + y_1x_1 - y_1x_3 + y_3x_1 - y_3x_3 + y_2x_2 - y_2x_1 + y_1x_2 - y_1x_1}{2}\\
&= \frac{-y_3x_2 + y_2x_3 - y_1x_3 + y_3x_1 - y_2x_1 + y_1x_2}{2}\\
&= \frac{y_1(x_2 - x_3) + y_2(x_3 - x_1) + y_3(x_1 - x_2)}{2}
\end{aligned}
A = A ( e 1 ) + A ( e 2 ) + A ( e 3 ) = 2 ( y 3 + y 2 ) ( x 3 − x 2 ) + ( y 1 + y 3 ) ( x 1 − x 3 ) + ( y 2 + y 1 ) ( x 2 − x 1 ) = 2 y 3 x 3 − y 3 x 2 + y 2 x 3 − y 2 x 2 + y 1 x 1 − y 1 x 3 + y 3 x 1 − y 3 x 3 + y 2 x 2 − y 2 x 1 + y 1 x 2 − y 1 x 1 = 2 − y 3 x 2 + y 2 x 3 − y 1 x 3 + y 3 x 1 − y 2 x 1 + y 1 x 2 = 2 y 1 ( x 2 − x 3 ) + y 2 ( x 3 − x 1 ) + y 3 ( x 1 − x 2 )
我们还可以进一步化简这个式子,因为我们可以在不影响面积的情况下平移三角形,比如将三角形垂直移动直到一点落在 x 轴上。例如当第三个点落到 x 轴上时,我们可以从每个 y 坐标中减去 y 3 y_3 y 3
A = y 1 ( x 2 − x 3 ) + y 2 ( x 3 − x 1 ) + y 3 ( x 1 − x 2 ) 2 = ( y 1 − y 3 ) ( x 2 − x 3 ) + ( y 2 − y 3 ) ( x 3 − x 1 ) + ( y 3 − y 3 ) ( x 1 − x 2 ) 2 = ( y 1 − y 3 ) ( x 2 − x 3 ) + ( y 2 − y 3 ) ( x 3 − x 1 ) 2 \begin{aligned}
A &= \frac{y_1(x_2 - x_3) + y_2(x_3 - x_1) + y_3(x_1 - x_2)}{2}\\
&= \frac{(y_1 - y_3)(x_2 - x_3) + (y_2 - y_3)(x_3 - x_1) + (y_3 - y_3)(x_1 - x_2)}{2}\\
&= \frac{(y_1 - y_3)(x_2 - x_3) + (y_2 - y_3)(x_3 - x_1)}{2}
\end{aligned}
A = 2 y 1 ( x 2 − x 3 ) + y 2 ( x 3 − x 1 ) + y 3 ( x 1 − x 2 ) = 2 ( y 1 − y 3 ) ( x 2 − x 3 ) + ( y 2 − y 3 ) ( x 3 − x 1 ) + ( y 3 − y 3 ) ( x 1 − x 2 ) = 2 ( y 1 − y 3 ) ( x 2 − x 3 ) + ( y 2 − y 3 ) ( x 3 − x 1 )
在三维中,可以使用叉积来计算三角形的面积,两个矢量 a {\bf a} a b {\bf b} b a {\bf a} a b {\bf b} b e 1 {\bf e_1} e 1 e 2 {\bf e_2} e 2
A = ∥ e 1 × e 2 ∥ 2 A = \frac{\lVert{\bf e_1 \times e_2}\rVert}{2}
A = 2 ∥ e 1 × e 2 ∥
重心空间
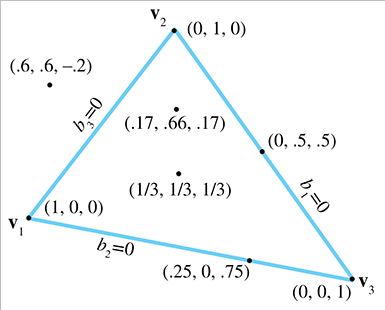
三角形平面中的任何点都可以表示为顶点的加权平均值。这些加权称为重心坐标。从重心坐标 (b 1 b_1 b 1 b 2 b_2 b 2 b 3 b_3 b 3
( b 1 , b 2 , b 3 ) ≡ b 1 v 1 + b 2 v 2 + b 3 v 3 (b_1, b_2, b_3) \equiv b_1{\bf v_1} + b_2{\bf v_2} + b_3{\bf v_3}
( b 1 , b 2 , b 3 ) ≡ b 1 v 1 + b 2 v 2 + b 3 v 3
重心坐标是一些矢量的线性组合,而普通笛卡尔坐标也可以解释为基矢量的线性组合,但重心坐标和普通笛卡尔坐标之间有一个细微的区别,那就是重心坐标的坐标之和被限制为 1,其定义如下:
b 1 + b 2 + b 3 = 1 b_1 + b_2 + b_3 = 1
b 1 + b 2 + b 3 = 1
值 b 1 b_1 b 1 b 2 b_2 b 2 b 3 b_3 b 3
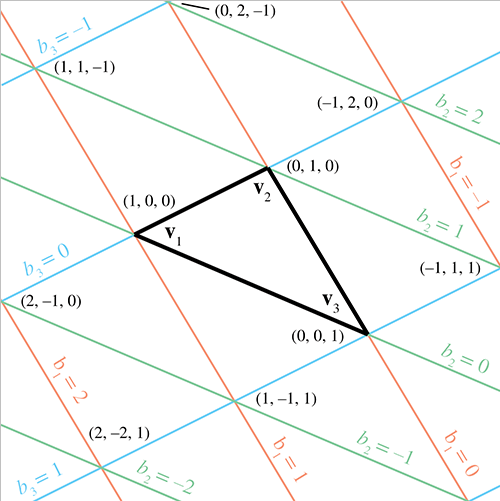
上图中的三角形的 3 个顶点在重心坐标中具有以下很简单的形式:
( 1 , 0 , 0 ) ≡ v 1 ( 0 , 1 , 0 ) ≡ v 2 ( 0 , 0 , 1 ) ≡ v 3 (1, 0, 0) \equiv {\bf v_1} \qquad (0, 1, 0) \equiv {\bf v_2} \qquad (0, 0, 1) \equiv {\bf v_3}
( 1 , 0 , 0 ) ≡ v 1 ( 0 , 1 , 0 ) ≡ v 2 ( 0 , 0 , 1 ) ≡ v 3
而且,与顶点相对的一条边上的所有点对应于该顶点的重心坐标将具有零值。例如,对于包含 e 1 {\bf e_1} e 1 v 1 {\bf v_1} v 1 b 1 = 0 b_1 = 0 b 1 = 0
平面中的任何点都可以用重心坐标来描述,而不仅仅是三角形内的点。三角形内部的点的重心坐标都在 [0, 1] 范围内,三角形外的任何点都将至少有一个负坐标值。重心空间可以将平面以与原始三角形大小相同的三角形来网格化,如下图所示。
还有另一种思考重心坐标的方法。丢弃 b 3 b_3 b 3 b 1 b_1 b 1 b 2 b_2 b 2 v 3 {\bf v_3} v 3 v 1 − v 3 {\bf v_1 - v_3} v 1 − v 3 v 2 − v 3 {\bf v_2 - v_3} v 2 − v 3
( b 1 , b 2 , b 3 ) ≡ b 1 v 1 + b 2 v 2 + b 3 v 3 ≡ b 1 v 1 + b 2 v 2 + ( 1 − b 1 − b 2 ) v 3 ≡ b 1 v 1 + b 2 v 2 + v 3 − b 1 v 3 − b 2 v 3 ≡ v 3 + b 1 ( v 1 − v 3 ) + b 2 ( v 2 − v 3 ) \begin{aligned}
(b_1, b_2, b_3) &\equiv b_1{\bf v_1} + b_2{\bf v_2} + b_3{\bf v_3}\\
&\equiv b_1{\bf v_1} + b_2{\bf v_2} + (1 - b_1 - b_2){\bf v_3}\\
&\equiv b_1{\bf v_1} + b_2{\bf v_2} + {\bf v_3} - b_1{\bf v_3} - b_2{\bf v_3}\\
&\equiv {\bf v_3} + b_1({\bf v_1 - v_3}) + b_2({\bf v_2 - v_3})
\end{aligned}
( b 1 , b 2 , b 3 ) ≡ b 1 v 1 + b 2 v 2 + b 3 v 3 ≡ b 1 v 1 + b 2 v 2 + ( 1 − b 1 − b 2 ) v 3 ≡ b 1 v 1 + b 2 v 2 + v 3 − b 1 v 3 − b 2 v 3 ≡ v 3 + b 1 ( v 1 − v 3 ) + b 2 ( v 2 − v 3 )
计算重心坐标
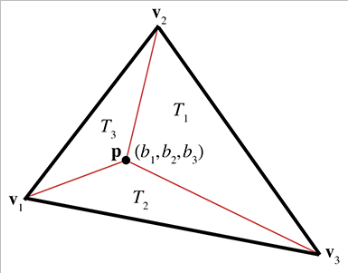
现在来看一看如何确定笛卡尔坐标的重心坐标。先从下图的二维开始,它显示了 v 1 {\bf v_1} v 1 v 2 {\bf v_2} v 2 v 3 {\bf v_3} v 3 p {\bf p} p T 1 T_1 T 1 T 2 T_2 T 2 T 3 T_3 T 3
已知 3 个顶点和点 p {\bf p} p b 1 b_1 b 1 b 2 b_2 b 2 b 3 b_3 b 3
b 1 x 1 + b 2 x 2 + b 3 x 3 = p x , b 1 y 1 + b 2 y 2 + b 3 y 3 = p y , b 1 + b 2 + b 3 = 1 \begin{aligned}
b_1x_1 + b_2x_2 + b_3x_3 &= p_x,\\
b_1y_1 + b_2y_2 + b_3y_3 &= p_y,\\
b_1 + b_2 + b_3 &= 1
\end{aligned}
b 1 x 1 + b 2 x 2 + b 3 x 3 b 1 y 1 + b 2 y 2 + b 3 y 3 b 1 + b 2 + b 3 = p x , = p y , = 1
求解该方程组得出以下结果:
b 1 = ( p y − y 3 ) ( x 2 − x 3 ) + ( y 2 − y 3 ) ( x 3 − p x ) ( y 1 − y 3 ) ( x 2 − x 3 ) + ( y 2 − y 3 ) ( x 3 − x 1 ) , b 2 = ( p y − y 1 ) ( x 3 − x 1 ) + ( y 3 − y 1 ) ( x 1 − p x ) ( y 1 − y 3 ) ( x 2 − x 3 ) + ( y 2 − y 3 ) ( x 3 − x 1 ) , b 3 = ( p y − y 2 ) ( x 1 − x 2 ) + ( y 1 − y 2 ) ( x 2 − p x ) ( y 1 − y 3 ) ( x 2 − x 3 ) + ( y 2 − y 3 ) ( x 3 − x 1 ) \begin{aligned}
b_1 &= \frac{(p_y - y_3)(x_2 - x_3) + (y_2 - y_3)(x_3 - p_x)}{(y_1 - y_3)(x_2 - x_3) + (y_2 - y_3)(x_3 - x_1)},\\
b_2 &= \frac{(p_y - y_1)(x_3 - x_1) + (y_3 - y_1)(x_1 - p_x)}{(y_1 - y_3)(x_2 - x_3) + (y_2 - y_3)(x_3 - x_1)},\\
b_3 &= \frac{(p_y - y_2)(x_1 - x_2) + (y_1 - y_2)(x_2 - p_x)}{(y_1 - y_3)(x_2 - x_3) + (y_2 - y_3)(x_3 - x_1)}\\
\end{aligned}
b 1 b 2 b 3 = ( y 1 − y 3 ) ( x 2 − x 3 ) + ( y 2 − y 3 ) ( x 3 − x 1 ) ( p y − y 3 ) ( x 2 − x 3 ) + ( y 2 − y 3 ) ( x 3 − p x ) , = ( y 1 − y 3 ) ( x 2 − x 3 ) + ( y 2 − y 3 ) ( x 3 − x 1 ) ( p y − y 1 ) ( x 3 − x 1 ) + ( y 3 − y 1 ) ( x 1 − p x ) , = ( y 1 − y 3 ) ( x 2 − x 3 ) + ( y 2 − y 3 ) ( x 3 − x 1 ) ( p y − y 2 ) ( x 1 − x 2 ) + ( y 1 − y 2 ) ( x 2 − p x )
可以看到每个表达式中的分母是相同的,而且由海伦公式的变形可知它等于三角形面积的两倍。而对于每个重心坐标 b i b_i b i T i T_i T i
b 1 = A ( T 1 ) / A ( T ) , b 2 = A ( T 2 ) / A ( T ) , b 3 = A ( T 3 ) / A ( T ) b_1 = A(T_1)/A(T),\qquad b_2 = A(T_2)/A(T),\qquad b_3 = A(T_3)/A(T)
b 1 = A ( T 1 ) / A ( T ) , b 2 = A ( T 2 ) / A ( T ) , b 3 = A ( T 3 ) / A ( T )
请注意,即使 p {\bf p} p
计算三维中任意点 p {\bf p} p p {\bf p} p p {\bf p} p
一个有效的技巧是,通过丢弃 x、y 或 z 中的一个来将三维问题转变为二维问题。这具有将三角形投影到 3 个基本平面之一上的效果。以直觉而言,这是有效的,因为投影面积与原始面积成正比。
但是,应该丢弃哪一个坐标呢?我们不能总丢弃相同的,因为如果三角形垂直于投影平面,投影点将是共线的。如果三角形几乎垂直于投影平面,那么将遇到浮点精度问题。解决这个问题的方法是选择投影平面,以便最大化投影三角形的面积。这可以通过检查平面法线来完成,具有最大绝对值的坐标就是我们将要丢弃的坐标。例如,如果法线是 [0.267, -0.802, 0.535],那么将丢弃顶点和 p {\bf p} p
下面代码展示如何计算任意三维点的重心坐标:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 bool computeBarycentricCoords3d ( const Vector3 v[3 ], const Vector3 &p, float b[3 ] ) {1 ] - v[0 ];2 ] - v[1 ];float u1, u2, u3, u4;float v1, v2, v3, v4;if ((fabs (n.x) >= fabs (n.y)) && (fabs (n.x) >= fabs (n.z))) {0 ].y - v[2 ].y;1 ].y - v[2 ].y;0 ].y;2 ].y;0 ].z - v[2 ].z;1 ].z - v[2 ].z;0 ].z;2 ].z;else if (fabs (n.y) >= fabs (n.z)) {0 ].z - v[2 ].z;1 ].z - v[2 ].z;0 ].z;2 ].z;0 ].x - v[2 ].x;1 ].x - v[2 ].x;0 ].x;2 ].x;else {0 ].x - v[2 ].x;1 ].x - v[2 ].x;0 ].x;2 ].x;0 ].y - v[2 ].y;1 ].y - v[2 ].y;0 ].y;2 ].y;float denom = v1*u2 - v2*u1;if (denom == 0.0f ) {return false ;float oneOverDenom = 1.0f / denom;0 ] = (v4*u2 - v2*u4) * oneOverDenom;1 ] = (v1*u3 - v3*u1) * oneOverDenom;2 ] = 1.0f - b[0 ] - b[1 ];return true ;
还有一种技术可以用于计算三维中的重心坐标,那就是使用叉积来计算三维三角形的面积的方法。给定三角形的两个边矢量 e 1 \bf e_1 e 1 e 2 \bf e_2 e 2 ∥ e 1 × e 2 ∥ / 2 \lVert{\bf e_1 \times e_2}\rVert /2 ∥ e 1 × e 2 ∥ /2
当然,这里有一个小问题:叉积的大小对顶点的排序不敏感——按照定义,其大小总是正的。那么三角形之外的点就不适用了,因为三角形之外的点必须始终至少有一个负重心坐标。看起来我们真正需要的是一种计算叉积矢量长度的方法,如果顶点以“不正确”的顺序枚举,则会产生负值。事实证明,使用点积有一种非常简单的方法。
假设将 c \bf c c c \bf c c n ^ \bf \hat{n} n ^ c \bf c c n ^ \bf \hat{n} n ^
c ⋅ n ^ = ∥ c ∥ ∥ n ^ ∥ cos θ = ∥ c ∥ ( 1 ) ( ± 1 ) = ± ∥ c ∥ \begin{aligned}
{\bf c} \cdot {\bf \hat{n}} &= \lVert {\bf c} \rVert \lVert {\bf \hat{n}} \rVert \cos\theta\\
&= \lVert {\bf c} \rVert(1)(\pm 1)\\
&= \pm \lVert {\bf c} \rVert
\end{aligned}
c ⋅ n ^ = ∥ c ∥ ∥ n ^ ∥ cos θ = ∥ c ∥ ( 1 ) ( ± 1 ) = ± ∥ c ∥
将此结果除以 2,就可以计算三维中三角形的“有符号面积”。
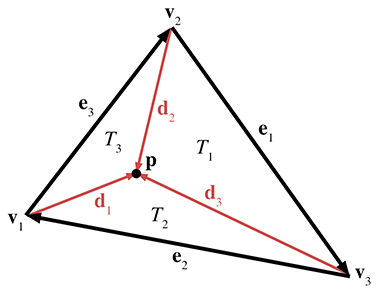
在上图中,每个顶点都有一个从 v i \bf v_i v i p \bf p p d i \bf d_i d i
e 1 = v 3 − v 2 e 2 = v 1 − v 3 e 3 = v 2 − v 1 d 1 = p − v 1 d 2 = p − v 2 d 3 = p − v 3 \begin{aligned}
{\bf e_1} &= {\bf v_3} - {\bf v_2} & {\bf e_2} &= {\bf v_1} - {\bf v_3} & {\bf e_3} &= {\bf v_2} - {\bf v_1}\\
{\bf d_1} &= {\bf p} - {\bf v_1} & {\bf d_2} &= {\bf p} - {\bf v_2} & {\bf d_3} &= {\bf p} - {\bf v_3}
\end{aligned}
e 1 d 1 = v 3 − v 2 = p − v 1 e 2 d 2 = v 1 − v 3 = p − v 2 e 3 d 3 = v 2 − v 1 = p − v 3
我们还需要一个表面法线,可以通过下式计算:
n ^ = e 1 × e 2 ∥ e 1 × e 2 ∥ \bf \hat{n} = \frac{e_1 \times e_2}{\lVert e_1 \times e_2 \rVert}
n ^ = ∥ e 1 × e 2 ∥ e 1 × e 2
现在整个三角形(简称为 T T T
A ( T ) = ( ( e 1 × e 2 ) ⋅ n ^ ) / 2 A ( T 1 ) = ( ( e 1 × d 3 ) ⋅ n ^ ) / 2 A ( T 2 ) = ( ( e 2 × d 1 ) ⋅ n ^ ) / 2 A ( T 3 ) = ( ( e 3 × d 2 ) ⋅ n ^ ) / 2 \begin{aligned}
A(T) &= (({\bf e_1 \times e_2})\cdot{\bf\hat{n}})/2\\
A(T_1) &= (({\bf e_1 \times d_3})\cdot{\bf\hat{n}})/2\\
A(T_2) &= (({\bf e_2 \times d_1})\cdot{\bf\hat{n}})/2\\
A(T_3) &= (({\bf e_3 \times d_2})\cdot{\bf\hat{n}})/2
\end{aligned}
A ( T ) A ( T 1 ) A ( T 2 ) A ( T 3 ) = (( e 1 × e 2 ) ⋅ n ^ ) /2 = (( e 1 × d 3 ) ⋅ n ^ ) /2 = (( e 2 × d 1 ) ⋅ n ^ ) /2 = (( e 3 × d 2 ) ⋅ n ^ ) /2
每个重心坐标 b i b_i b i A ( T i ) / A ( T ) A(T_i)/A(T) A ( T i ) / A ( T )
b 1 = A ( T 1 ) / A ( T ) = ( e 1 × d 3 ) ⋅ n ^ ( e 1 × e 2 ) ⋅ n ^ b 2 = A ( T 2 ) / A ( T ) = ( e 2 × d 1 ) ⋅ n ^ ( e 1 × e 2 ) ⋅ n ^ b 3 = A ( T 3 ) / A ( T ) = ( e 3 × d 2 ) ⋅ n ^ ( e 1 × e 2 ) ⋅ n ^ \begin{aligned}
b_1 = A(T_1)/A(T) = \frac{({\bf e_1 \times d_3})\cdot{\bf\hat{n}}}{({\bf e_1 \times e_2})\cdot{\bf\hat{n}}}\\
b_2 = A(T_2)/A(T) = \frac{({\bf e_2 \times d_1})\cdot{\bf\hat{n}}}{({\bf e_1 \times e_2})\cdot{\bf\hat{n}}}\\
b_3 = A(T_3)/A(T) = \frac{({\bf e_3 \times d_2})\cdot{\bf\hat{n}}}{({\bf e_1 \times e_2})\cdot{\bf\hat{n}}}\\
\end{aligned}
b 1 = A ( T 1 ) / A ( T ) = ( e 1 × e 2 ) ⋅ n ^ ( e 1 × d 3 ) ⋅ n ^ b 2 = A ( T 2 ) / A ( T ) = ( e 1 × e 2 ) ⋅ n ^ ( e 2 × d 1 ) ⋅ n ^ b 3 = A ( T 3 ) / A ( T ) = ( e 1 × e 2 ) ⋅ n ^ ( e 3 × d 2 ) ⋅ n ^
请注意,n ^ \bf \hat{n} n ^
特殊点
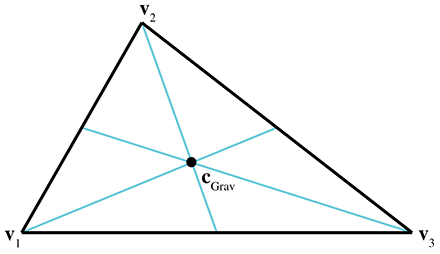
重心
重心是三角形完美的平衡点,它是中线的交点(中线是从一个顶点到对边中点的直线)。
重心是 3 个顶点的几何平均值:
c G r a v = v 1 + v 2 + v 3 3 {\bf c_{Grav}} = \frac{\bf v_1 + v_2 + v_3}{3}
c Grav = 3 v 1 + v 2 + v 3
重心坐标为:
( 1 3 , 1 3 , 1 3 ) (\frac{1}{3}, \frac{1}{3}, \frac{1}{3})
( 3 1 , 3 1 , 3 1 )
重心也被称为质心。
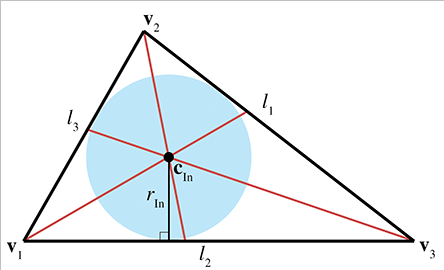
内心
三角形的内心是三角形 3 条角平分线的焦点,它之所以被称为内心,是因为它也是三角形内切圆的圆心。由该特性可知,内心与三角形各条边的距离是相等的。
内心可通过下式计算:
c I n = l 1 v 1 + l 2 v 2 + l 3 v 3 p {\bf c_{In}} = \frac{l_1{\bf v_1} + l_2{\bf v_2} + l_3{\bf v_3}}{p}
c In = p l 1 v 1 + l 2 v 2 + l 3 v 3
其中,p = l 1 + l 2 + l 3 p = l_1 + l_2 + l_3 p = l 1 + l 2 + l 3
( l 1 p , l 2 p , l 3 p ) (\frac{l_1}{p}, \frac{l_2}{p}, \frac{l_3}{p})
( p l 1 , p l 2 , p l 3 )
可以通过下式将三角形的面积除以其周长来计算内切圆的半径:
r I n = A p r_{In} = \frac{A}{p}
r I n = p A
内切圆解决了找到与 3 条线相切的圆的问题。
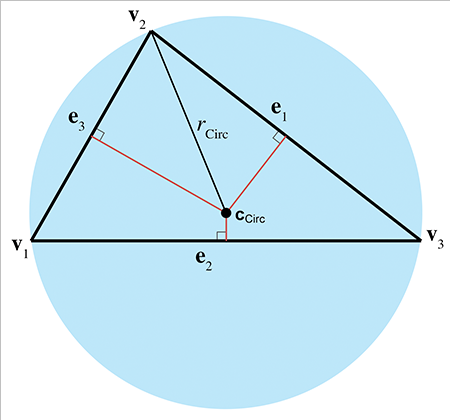
外心
外心是三角形中与顶点等距的点,它是围绕三角形的外接圆的圆心。外心构造为各条边的垂直平分线的交点。
要计算外心,需要先定义以下的中间值:
d 1 = − e 2 ⋅ e 3 , d 2 = − e 3 ⋅ e 1 , d 3 = − e 1 ⋅ e 2 , c 1 = d 2 d 3 , c 2 = d 3 d 1 , c 3 = d 1 d 2 , c = c 1 + c 2 + c 3 \begin{aligned}
d_1 &= -{\bf e_2}\cdot{\bf e_3},\\
d_2 &= -{\bf e_3}\cdot{\bf e_1},\\
d_3 &= -{\bf e_1}\cdot{\bf e_2},\\
c_1 &= d_2d_3,\\
c_2 &= d_3d_1,\\
c_3 &= d_1d_2,\\
c &= c_1 + c_2 + c_3
\end{aligned}
d 1 d 2 d 3 c 1 c 2 c 3 c = − e 2 ⋅ e 3 , = − e 3 ⋅ e 1 , = − e 1 ⋅ e 2 , = d 2 d 3 , = d 3 d 1 , = d 1 d 2 , = c 1 + c 2 + c 3
在取得这些中间值后,即可按下式给出外心的重心坐标:
( c 2 + c 3 2 c , c 3 + c 1 2 c , c 1 + c 2 2 c ) (\frac{c_2 + c_3}{2c}, \frac{c_3 + c_1}{2c}, \frac{c_1 + c_2}{2c})
( 2 c c 2 + c 3 , 2 c c 3 + c 1 , 2 c c 1 + c 2 )
由此,外心可通过下式计算:
c C i r c = ( c 2 + c 3 ) v 1 + ( c 3 + c 1 ) v 2 + ( c 1 + c 2 ) v 3 2 c {\bf c_{Circ}} = \frac{(c_2 + c_3){\bf v_1} + (c_3 + c_1){\bf v_2} + (c_1 + c_2){\bf v_3}}{2c}
c Circ = 2 c ( c 2 + c 3 ) v 1 + ( c 3 + c 1 ) v 2 + ( c 1 + c 2 ) v 3
外接圆半径的计算公式为:
r C i r c = ( d 1 + d 2 ) ( d 2 + d 3 ) ( d 3 + d 1 ) / c 2 r_{Circ} = \frac{\sqrt{(d_1 + d_2)(d_2 + d_3)(d_3 + d_1)/c}}{2}
r C i rc = 2 ( d 1 + d 2 ) ( d 2 + d 3 ) ( d 3 + d 1 ) / c
外接圆半径和外心解决了找到通过三个点的圆的问题。